Рассматривается электрическая схемная модель узла теплогидравлической системы электростанции [1], представляющая собой двухконтурную резонансную цепь с нелинейной связью, находящуюся под периодическим воздействием. Такая модель является типовой, поскольку теплогидравлические системы имеют нелинейные характеристики и постоянно подвергаются вибрациям, вызванным как работой двигателей, турбин, насосов, так и турбулентными движениями самих перекачиваемых жидкостей и пароводяных смесей. Возникают различные типы колебаний нелинейных систем, которые в некоторых случаях могут привести к аварии. В данной работе с целью диагностики оборудования анализируется процесс возникновения комбинационных колебаний в двухконтурной электрической модели (рис. 1), представляющей собой соединение источника ЭДС, двух параллельных резонансных контуров с различными частотами и нелинейного индуктивного элемента, вебер-амперная характеристика которого аппроксимирована кубическим полиномом

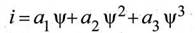
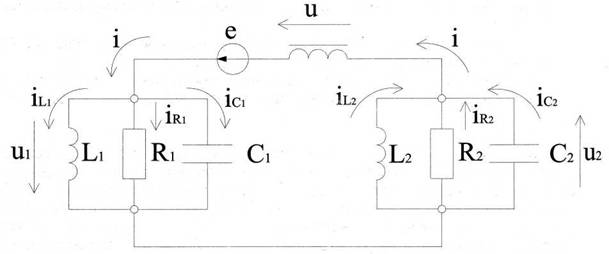
Рис. 1

В такой цепи при определенном соотношении резонансных частот системы, частоты и амплитуды воздействующей периодической ЭДС возможна генерация комбинационных колебаний на двух частотах, в сумме равных частоте источника ЭДС. Возможна также генерация колебаний типа феррорезонансных на частоте источника. Возможно и сложное взаимодействие этих процессов, проявляющееся в виде хаотических колебаний, которые наблюдаются в эксперименте. Сложные колебания в теплогидравлической системе сопряжены с большими механическими усилиями, что может привести к нарушению прочности или устойчивости конструкции. Задача электрического моделирования - прогнозирование и предотвращение таких эффектов.

Моделирование проводится по методу усреднения. Укороченные уравнения для комбинационных колебаний в двухконтурной цепи составляются по методике, изложенной в [2]. Комбинационные колебания возбуждаются на частотах, близких к нормальным. Как известно, при этом определяется только суммарная фаза комбинационных колебаний. Укороченные уравнения в нормальных координатах имеют вид

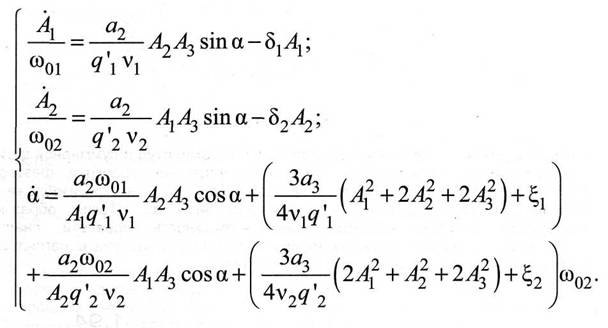
Здесь А1, А2 - амплитудные значения нормальных координат; A3 -относительная нормированная амплитуда ЭДС источника; α = φ1 + φ2 -суммарная фаза комбинационных колебаний; ω01, ω02 - нормальные частоты; v1, v2 - частоты возбуждаемых колебаний; σ1, σ 2 - коэффициенты затухания; ξ1, ξ2 - расстройки частот генерации относительно нормальных частот; q'1, q'2 - коэффициенты, определяемые линейными параметрами цепи. В данной работе рассматривается цепь в режиме возбуждения комбинационных колебаний (условия возбуждения были получены в [3]). Ставится задача расчета установления колебаний и построения фазовой траектории этого процесса. Определенная трудность состоит в том, что исследуется система нелинейных уравнений с тремя неизвестными. Соответственно фазовая траектория должна представлять собой сложную пространственную кривую. Для решения такой задачи использована программная среда LabVIEW. Составлена программа численного решения системы укороченных уравнений. Полученная в результате расчета фазовая траектория в пространстве Ван дер Поля построена при помощи трехкоординатного осциллографа. Общий вид полученной траектории представлен на рис. 2.

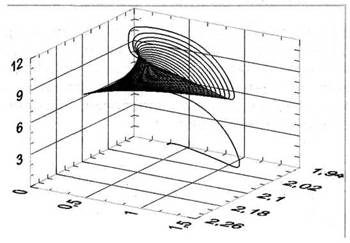
Рис.2

Процессы установления каждой из переменных - амплитуд и суммарной фазы комбинационных колебаний - можно наблюдать как проекции фазовой траектории на координатные плоскости. Так, на рис. 3 изображено установление амплитуды А1 и суммарной фазы а. Таким образом, применение системы LabVIEW дает возможность провести анализ укороченных уравнений сложных нелинейных цепей и получить наглядную картину установления комбинационных колебаний.

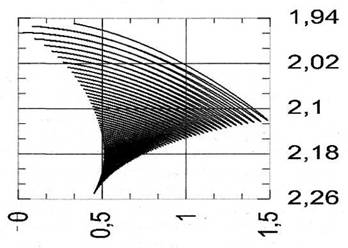
Рис. 3

Список Литературы

1. Проскуряков К.Н. Использование виброакустических шумов для диагностики процессов в АЭС. - М.: Издательство МЭИ, 1999. - 68 с.

2. Каплан А.Е., Кравцов Ю.А., Рылов В.А. Параметрические генераторы и делители частоты. - М.: Сов. Радио,1966. - 336 с.

3. Золотухин И.А. Экспериментальное исследование колебательных процессов в электрической модели теплогидравлической системы. - Межд. научно-практ. конф. «Образовательные, научные и инженерные приложения в среде LabVIEW». Сб. трудов конф. - М.: Изд. РУДН, 2005. - С. 150-154.