Постановка задачи

Использование для технических измерений массово производимых видео- и фотокамер, не предназначенных специально для индустриальных применений, обусловлено их невысокой стоимостью и достаточно высокими техническими характеристиками. Основной проблемой является отсутствие данных о нормированных метрологических характеристиках таких камер. В работе показан пример решения этой проблемы на основе дифференциального метода измерений. Показана возможность адаптации к производственным условиям с применением программных продуктов National Instruments. Показана возможность минимизации ошибок первого рода применением измерительного контроля.

Описание решения

Схема измерений. Решается измерительная задача, требуется получить двумерное изображение и выполнить идентификацию объекта и определить его геометрические параметры. Объект представляет собой кольцо с внутренним диаметром d и наружным диаметром D, средняя площадь объекта ориентировочно составляет 1 мм². Толщина ориентировочно составляет 0,3 мм.

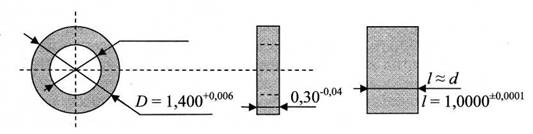
Рис. 1. Размеры объекта контроля (D, d) и эталона (/)

Размеры и внешний вид объекта контроля и эталона, использованного для дифференциальных измерений, приведены на рис. 1. Для идентификации основных источников погрешности разработана базовая схема измерений, представленная на рис. 2.

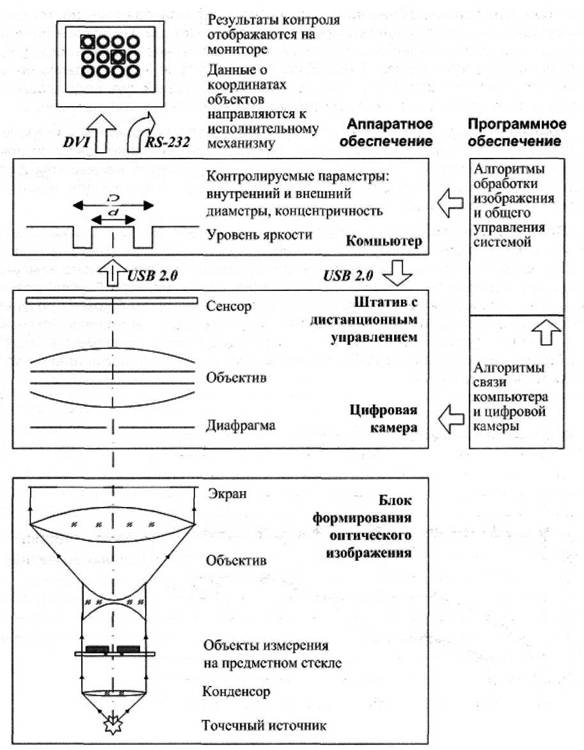
Рис. 2. Базовая схема измерений

Блок формирования оптического изображения (БФОИ) формирует изображение, удобное для наблюдения оператором и в то же время, адаптированное для восприятия цифровой камерой. Свет от лампы проходит через линзы постоянного конденсора и падает на предметное стекло, где в поле 10 × 13 мм устанавливаются объекты измерения. Далее лучи попадают в объектив, который проецирует на экран увеличенное теневое изображение.

Цифровая камера преобразует двумерное оптическое изображение в цифровую форму и размещает для обработки и хранения в виде файла на жестком диске компьютера. Диафрагма, объектив и штатив имеют фиксированные настройки для заданной точности и производительности измерений. Сенсор изготовлен по нормам субмикронного технологического процесса и представляет собой геометрически прецизионный аналого-цифровой преобразователь. Встроенное программное обеспечение преобразует сигналы в последовательный двоичный код, содержащий сведения об уровне яркости как основном сигнале измерительной информации.

Компьютер выполняет идентификацию и адресацию объектов измерения. В зависимости от программного алгоритма, выполняются операции контроля или измерения с погрешностью ±1-2 мкм, результаты сохраняются на жестком диске и отображаются на мониторе, формируются управляющие сигналы для механизмов перемещения объектов измерения.

Влияние фильтрации на результаты измерений.

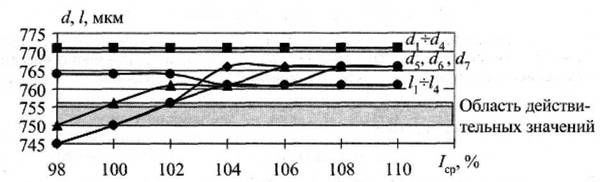
На рис. 1 кольцо изображает объекты контроля, прямоугольник изображает объекты, используемые для калибровки. В соответствии с математической моделью [1, 2] выполнено компьютерное моделирование и экспериментальное исследование фильтра Гаусса, результаты представлены на рис. 2. Группа из трех графиков d₅-d₇ отображает результаты эксперимента для трех кольцевых объектов. Погрешность ε₃, вызванная загрязнением объектов измерения, представлена на рис. 2 разбросом экспериментальных кривых d₅-d₇ - Применение фильтра Гаусса уменьшает ε₃ втрое на номинальном уровне силы света (I_ср = 100 %) [3].

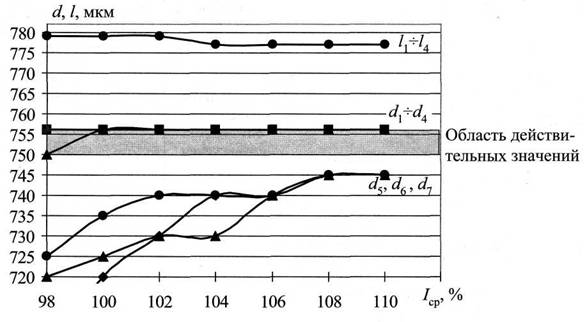
а)

б)

Рис. 2. Результаты измерения внутреннего диаметра d часовых камней при изменении силы света (а - результаты модельных d₁-d₄, I₁-I₄ и реальных d₅,d₆,d₇ измерений; б - те же результаты при использовании фильтра Гаусса)

Очевидно, что применение сглаживающего фильтра существенно уменьшает разброс результатов измерения. Для сглаживания предпочтительно использовать гауссиан, по следующим причинам. Во-первых, если выполнить свертку гауссиана с гауссианом, получим еще один гауссиан. Следовательно, можно получить сильно сглаженное изображение, повторно сгладив уже сглаженное изображение. Так могут быть получены варианты изображения с различной степенью сглаживания. Во-вторых, повторное сглаживание эффективнее расходует вычислительный ресурс, т.к. приходится оперировать не столь значительными массивами данных. В третьих, многократная свертка положительного ядра любого распределения с самим собой в результате дает ядро, которое будет гауссианом [4].

На рис. 2 представляет интерес область I_ср = (108-110) %. Это область фильтрации «геометрических шумов» согласно [5]. В основе фильтрации лежит диффузное рассеивание света в матовом слое.

Программно-алгоритмическое обеспечение

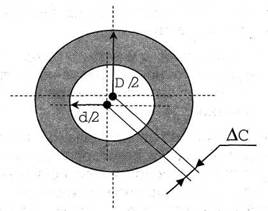
Рис. 3. Измеряемые параметры объекта контроля

Находятся координаты C_D и с _d центров массы окружностей D и d [82].

После того как шумы отфильтрованы и границы объекта определены, находятся геометрические параметры объекта измерения. Программным алгоритмом реализовано виртуальное средство измерений в среде LabVEW . Для объекта в форме кольца выполняется измерение наружного диаметра D и диаметра отверстия d, межцентровых расстояний (концентричности) ∆с в соответствии с рис. 3.

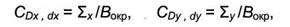
где Σ_х- сумма координат х всех пикселей, расположенных на окружности, Σ_У- сумма координат у всех пикселей, расположенных на окружности, В_окр - число пикселей, расположенных на окружности. Находится межцентровое расстояние

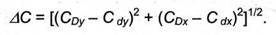
Находятся диаметры D и d

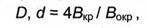
где В_кр - число пикселей, расположенных в круге.

Внедрение и развитие решения

Рассмотренные выше решения апробированы экспериментально. Дальнейшее развитие полученных решений могло бы включать минимизацию ошибок первого рода и увеличение процента выхода годных деталей по результатам контроля.

Минимизация ошибок первого рода.

Соотношения (1)-(3), положенные в основу алгоритма измерений, ориентированы на исключение ошибок второго рода. Этот подход характерен для контроля посредством предельных шаблонов или калибров. Применение измерительного контроля дополнительно дает возможность минимизации ошибок первого рода.

Рис. 4.

Контролируемые параметры: внутренний и внешний диаметр, концентрич ность. На рис. 4а изображен объект измерения, изгоровленный без искажения кон тролируемых параметров. Возможны следующие варианты искажения этих пара метров: пропорциональное искажение диаметров (рис. 46), искажение концентрич ности (рис. 4в), непропорциональное искажение диаметров (рис. 4 г), а также комби нация этих вариантов (рис. 4д).

При комбинации вариантов возможны два предельных случая: 1) искажения суммируются и достигают максимального значения. 2) искажения компенсируются и достигают минимального значения.

Первый случай наихудший, с учетом его, как правило, формируется техническое задание. При заданной точности измерения и при заданных значениях допустимого отклонения контролируемых параметров, деталь остается пригодной даже при суммировании искажений.

Второй случай наилучший, он, как правило, не учитывается техническим заданием, т.е. допускается отбраковка некоторого количества годных деталей (ошибка первого рода), для упрощения процесса контроля. Разработка алгоритма измерений, позволяющего проводить интегральное измерение по всем вариантам искажения параметров и на этой основе учитывать взаимную компенсацию искажений, позволила бы минимизировать ошибки первого рода. Программно-алгоритмические средства, предоставляемые National Instruments, в частности, определение эллиптических параметров объекта измерения, позволяют минимизировать ошибки первого рода.

Список литературы

[1] National Instruments. Vision. Documentation. IMAQ Vision Concepts Manual [Электронный ресурс] ; Worldwide Technical Support and Product Information / National Instruments Corporate Headquarters. — June 2003 Edition. — Electronic text and graphic data (1 file : 8 Mbytes). — Austin Texas USA : National Instruments Corporation, 2003. — Систем, требования: Windows XP/2000/NT/Me/9x. — Part Number 322916S-01.

[2] Николаев, М. И. Математическая модель системы технического зрения для гео метрических микроизмерений [Текст] / М. И. Николаев //Электронное приборострое ние. Научно-практический сборник. Выпуск 2(47). — Казань: ЗАО «Новое знание», 2006. — С. 64-76.

[3] Решение от 22.03.2007 о выдаче патента на изобретение согласно заявки 2005140712/28(045339) РФ. Способ компенсации погрешности масштабирования системы технического зрения для микроизмерений / Евдокимов Ю. К., Николаев М. И., Доронин А. Н. (РФ).

[4] Форсайт, Д. А. Компьютерное зрение. Современный подход [Текст]: [пер. с англ.] / Дэвид А. Форсайт, Ж. Понс. — М. [и др.]: Вильяме, 2004. — 928 с.

[5] Николаев, М. И. Аппаратная реализация системы технического зрения для измерения геометрии микрообъектов [Текст] / М. И. Николаев // Электронное приборостроение. Научно-практический сборник. Выпуск 3(44). — Казань: ЗАО «Новое знание», 2005.—С. 19-29.