LabWindows/CVI 8.0 и LabVIEW 8.0, предоставляющие средства быстрой разработки приложений пользователя в сфере систем измерения и управления, ценен и тем, что содержит библиотеку сложных видов математической обработки. Многие средства частотного анализа, включая БПФ, оконную фильтрацию позволяют решать задачи анализа спектров, не прибегая к специальным программам, таким как MATLAB.

Объединение усилий программистов по дополнению библиотеки сложных видов математической обработки LabWindows/CVI 8.0 и LabVIEW 8.0, так же, как это делается, например, в отношении MATLAB, было бы весьма полезно пользователям во всем мире[1].

Задача вычисления точного значения количества периодов и частоты дискретизированного сигнала является весьма актуальной при спектральном анализе сигналов спектрометров. Частотный спектр сигнала в этом случае характеризует состав изучаемого вещества, так как каждое вещество (химический элемент) характеризуется строго индивидуальной резонансной частотой. Частотный спектр сигнала нужно определять максимально точно, поскольку частотные линии разных веществ могут находиться весьма близко.

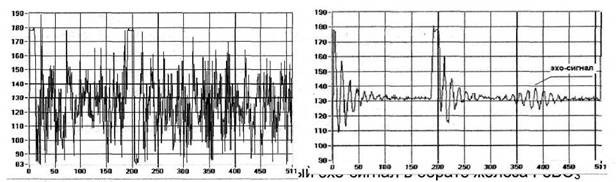
Известным и широко используемым программным средством спектрального анализа является быстрое преобразование Фурье (БПФ). Результатом БПФ дискретизированного сигнала определенной частоты является количество периодов сигнала. Если частота отсчетов или интервал дискретности по времени при измерении сигнала известен, то по количеству периодов можно определить и частоту измеряемого сигнала. Точность определения частоты в спектре входного сигнала является вполне определенной и зависит от количества периодов р сигнала. Если количество периодов целое, то частота с помощью БПФ определяется абсолютно точно (при отсутствии зашумленности сигнала). Если же количество периодов не является целым, то появляется погрешность определения частоты. Максимальное значение погрешности равняется 1/р. В некоторых, практически важных случаях, например, при обработке эхо-сигналов (Рис. 1) импульсных спектрометров ядерного магнитного резонанса, количество периодов анализируемого сигнала принципиально ограничено величиной около 10 [2]. В этом случае погрешность определения частоты с помощью БПФ достигает 1/10, т.е. 10%. Непосредственное использование БПФ для зашумленного сигнала не позволяет получить точное значение количества периодов и частоты измеряемого сигнала, в частности, в том случае, когда количество периодов не является целым. Когда анализируемый сигнал занимает только часть временной области, модулирован по амплитуде и зашумлен, частотный спектр сигнала будет зашумлен тоже (см. рис. 3).В этих условиях частотный анализ с помощью БПФ становится весьма трудным, а может стать и невозможным.

1. Постановка задачи

Усовершенствование алгоритма БПФ с целью повышения точности определения количества периодов и частоты дискретизированного сигнала в условиях, когда обрабатываемый сигнал зашумлен, количество периодов не является целым, сигнал модулирован по амплитуде, количество периодов сигнала во временной области мало.

2. Описание решения

Основой предлагаемого нами в [3] алгоритма является обработка массива спектра БПФ. Обработка заключается в нахождении методами оптимизации параметров аппроксимирующей зависимости для массива спектра в предложенном нами классе функций, соответствующих типичным ЯКР-спектрам наркотических и взрывчатых веществ. Алгоритм исследован при обработке реальных сигналов в диапазоне частот от 1 до 5 МГц и в режиме компьютерного моделирования. Для регистрации сигналов использовался быстродействующий АЦП с памятью, имеющий частоту отсчетов 50 МГц. Экспериментальные исследования показали, что предлагаемый алгоритм имеет значительные преимущества при значительно зашумленном спектре и позволяет определять значения частоты с точностью порядка 1% даже в тех случаях, когда известные методы, основанные на БПФ, бессильны.

Ниже, на рис. 2, в качестве примера, приведены экранная форма предлагаемой программы и результаты обработки сигнала.

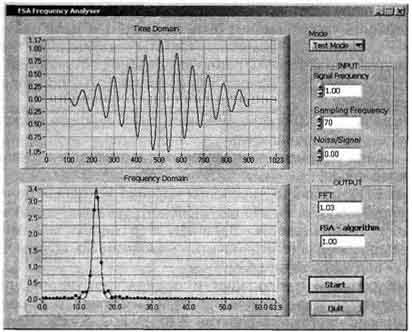
Рис. 2. Экранная форма программы частотного анализа

На рис. 3 приведены результаты обработки такого же по форме, но зашумленного сигнала. Амплитуда шума превышает амплитуду сигнала в два раза.

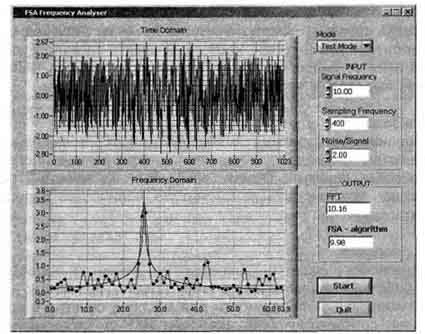
Рис. 3. Пример обработки зашумленного сигнала

Назначение элементов управления и ввода/вывода:

Mode - позволяет выбрать режим работы программы - Test Mode или Main Mode. В режиме Test Mode формирование анализируемого дискретизированного (т.е. представленного в виде числового массива) тестового сигнала производится в программе. В режиме Main Mode анализируемый дискретизированный сигнал считывается из файла.

Noise/Signal - окно для ввода отношения шум/сигнал в режиме Test Mode.

Signal Frequency - окно для ввода частоты сигнала в режиме Test Mode. Размерность частоты может быть любой (Гц, кГц, МГц), но она должна совпадать с размерностью частоты отсчетов, задаваемой в окне Sampling Frequency.

Sampling Frequency - окно для ввода частоты отсчетов в режиме Test Mode и Main Mode. Размерность частоты может быть любой (Гц, кГц, МГц).

FFT - окно для вывода значения частоты, полученной с помощью БПФ. Используется стандартный алгоритм, реализованный в LabWindows/CVI и LabVIEW.

FSA-algorithm - окно для вывода значения частоты, полученной с помощью предлагаемого алгоритма.

Предлагаемая нами в [3] программа частотного анализа дискретизированного сигнала реализует следующий алгоритм.

1. Чтение из файла рабочего числового массива исходных данных X[i], i=0,..M, M=2ⁿ, n-целое число.

2. Выполнение БПФ рабочего числового массива исходных данных X[i], i=0,..M, M=2ⁿ, n-целое число, и получение числового массива частотного спектра Y[j], j=1...s, s<=2ⁿ . Примечание. Величину s с целью минимизации времени обработки целесообразно ограничить максимально возможным ожидаемым количеством периодов сигнала X[i]

3. Выполнение сплайн-интерполяции и передискретизации для массива Y[j], j=1...s, с увеличением количества точек массива в К раз. В результате получаем массив частотного спектра Z(p), p=1..S, S=s*K. Количество точек в этом массиве больше в К раз, чем в массиве Y[j].

4. Аппроксимация числового массива Z(p) специальной аналитической зависимостью f(p) [3] путем нахождения численных значений коэффициентов этой зависимости а, Ь, с, d методом оптимизации по алгоритму Гаусса-

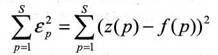
Зейделя с фиксированным количеством N шагов по принципу минимизации суммы квадратов отклонений функций z(p) и f(p):

5. Вычисление уточненного (в общем случае нецелого) значения количества периодов в числовом массиве исходных данных X[i]):

Q = b/K и частоты:

f= Q/(dt*M),

где dt - шаг дискретности по времени при измерении сигнала X(t), вычисляется как величина, обратная частоте отсчетов при измерении;

М - количество значений дискретизированного сигнала в массиве X[i]

Точность определения основной частоты при использовании предложенного алгоритма зависит от значений К и N и тем выше, чем больше значения К и N, однако, если анализируемый сигнал зашумлен, существенное увеличение точности определения частоты происходит при увеличении К и N лишь до некоторого предела. В частности, при соотношении сигнал/шум 1/1 - 1/2, К=10 и N=200, как показали наши исследования, оказывается наилучшим выбором по критерию точность/время анализа.

Предлагаемый алгоритм позволяет получить значение частоты дискретизированного сигнала с точностью до 3 десятичных разрядов даже при отношении сигнал/шум 1:1.

3. Используемое оборудование и ПО

Алгоритм исследован нами как в режиме компьютерного моделирования в среде LabWindows/CVI 8.0, так и при обработке реальных сигналов в диапазоне частот от 1 до 5 МГц [3]. Для регистрации сигналов использовался быстродействующий АЦП с памятью ЛА_н10М6РС1 (50 МГц, 2 канала, 256 Кбайт памяти).

4. Внедрение и развитие решения

Разработка предназначена для использования в системах обнаружения и идентификации веществ методами ядерного магнитного и ядерного квадрупольного резонанса.

Быстрому и своевременному выполнению данной разработки способствовали возможности систем проектирования LabWindows/CVI 8.0 и LabVIEW 8.O. Использование LabWindows/CVI 8.0 дало возможность в короткий срок отработать алгоритм частотного анализа и создать dll-библиотеку за счет многочисленных сервисов при создании программного кода и средств интерфейса пользователя. LabVIEW 8.0 - прекрасная среда для разработки приложений пользователя, поскольку предоставила возможность быстрого создания сложных программ и допускает пополнение библиотек функций разработчиком.

Литература

1. Пьер Бернард. Повысьте скорость ваших измерений с помощью более мощных алгоритмов. //National Instruments Instrumentation newsletter. 2000/2001.

2. В.И.Тарханов, B.C. Тутыгин Приборный комплекс для поиска и исследования сигналов ЯМР в магнитоупорядоченных веществах. // Научное приборостроение, 2003, том 13, №1, с.58-63, ISSN 0868-5886.

3. Тутыгин B.C., Шедов СВ. Программа частотного анализа дискретизированного сигнала. Свид. № 2007613363 от 09.10.2007 о Гос. регистрации программы.

4. Дебелова А.В., Тутыгин B.C. Программа определения точных значений количества периодов и частоты дискретизированного сигнала. Свид. № 2007612320 от 01.06.2007 о Гос. регистрации программы.