Учебный практикум "Спектральный и корреляционный анализ"
Аннотация.
Цель задачи - ознакомить с применением корреляционных и спектральных методов обработки на примере выделения периодического сигнала из шума. Задача состоит из подробного теоретического введения и 8 практических упражнений.
Введение
Необходимость, достоинства и широта применения спектрального и корреляционного анализа общеизвестны, поэтому подробного введение с доказательством и обсуждением этих фактов можно пропустить. Отметим только необходимость познакомить огромное количество студентов с дискретным преобразованием Фурье и вычислением автокорреляционной функции. Причем не просто познакомить, а найти способ сделать так, чтобы они запомнили это на всю оставшуюся жизнь или, по крайней мере, время обучения и, желательно, работы. Над этой нелегкой задачей бьется уже не первое поколение преподавателей во ВСЕХ вузах с преподаванием естественных наук ВСЕХ стран.
Данная задача - еще одно средство обучения студентов. В нее входит подробное теоретическое введение, написанное на основе классических книг по спектральному и корреляционному анализу. Но основной частью является практическая, в которую входит 8 упражнений с оборудованием. Эти упражнения позволяют изучить эффект наложения частот, влияние модуляции сигнала на его спектр, выделить сигнал из шума несколькими методами и закрепить другие базовые особенности спектрального и корреляционного анализа.
Состав задачи
Основные части задачи любого современного практикума - описание, аппаратные средства и программное обеспечение. В описании задачи содержится теоретическое введение, достаточное для выполнения задачи и описание ряда упражнений практикума. Аппаратные средства задачи должны быть максимально универсальными, подходящими для выполнения различных работ, но не в ущерб функциональности. Для этого большая часть функциональности задачи должна ложиться на программное обеспечение. Все уже узнали основное свойство виртуальных приборов National Instruments LabVIEW.
Описание аппаратного обеспечения.
Благодаря технологиям National Instruments, оборудование задачи (кроме персонального компьютера) получилось свести к одному прибору. Это плата ввода/вывода данных Nl PCI-6224, Nl PCI-6221 или аналогичная. Для удобства коммутации используется соединительная панель (BNC-2090 или аналогичная). Для задачи требуется по одному каналу ввода и вывода данных.
Студенту не требуется выполнять переключение каналов генерации или регистрации данных. Основная работа выполняется на персональном компьютере с виртуальными приборами. Согласитесь, что срок службы оборудования в этом случае возрастает.
Теоретическое введение
Это необходимая часть любой задачи. Теоретическое введение данной задачи состоит из двух основных частей: спектральный анализ и корреляционный анализ. Они включают в себя формулы, их объяснение, необходимые для понимания задачи. Разумеется, требуется базовая подготовка студента: понятия время, спектр и частота в задаче используются, а не объясняются.
Спектральный анализ
Спектральный анализ экспериментальных результатов проводится на ЭВМ с использованием аппарата конечного преобразования Фурье (КПФ). Непрерывная функция X(t) заменяется дискретной функцией U(j)=X(t0j), заданной в моменты времени t(j)=t0j, где t0 - шаг дискретизации, j - номер отсчета. Согласно теореме Котельникова периодическая функция с ограниченным спектром fv может быть однозначно восстановлена по дискретной функции, заданной в отсчетах, если шаг дискретизации удовлетворяет неравенству to<1/(2- fv).
Спектр дискретной функции, конечного анализа Фурье (КАФ), является периодической функцией, период которой по частоте равен 1/t0. Частота fN=1/(2t0) называется частотой Найквиста. Расстояние по оси частот между гармониками спектра δf=1/T=1/(t0·N) определяется интервалом времени, на котором определена функция U(j).
Если шаг дискретизации t0>1/(2fv) (fv>fN), то спектр дискретной функции оказывается искаженным и отличается от спектра непрерывной функции вследствие так называемого эффекта наложения частот.
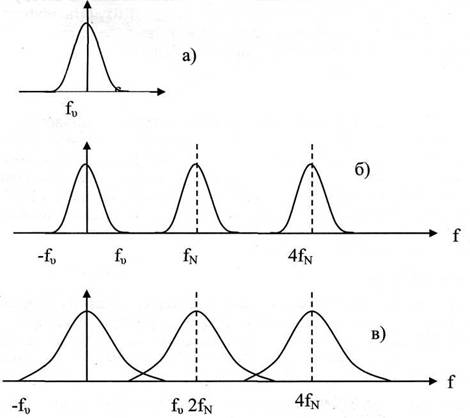
Рисунок 1. Эффект наложения частот, возникающий при дискретизации функции:
а) спектр непрерывной функции;
б) спектр дискретной функции (fv<1/(2t0) (fv<fN)',
в) спектр дискретной функции fv>1/(2t0) (fv>fN)
Для вычисления спектра дискретной функции используется алгоритм БПФ, позволяющий существенно сократить количество требуемых операций. Так, вычисление N спектральных компонент непосредственно по формуле для спектра требует порядка N2 комплексных операций типа сложения и умножения, в то время как использование алгоритма БПФ требует N·log2N операций.
Основными характеристиками выборочной спектральной плотности мощности (СПМ) являются ее состоятельность и смещение.
Если функция U(t) является детерминированной, то выборочная СПМ является состоятельной и асимптотически несмещенной оценкой истинной СПМ S(f), т.е.
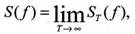
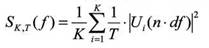
Истинная СПМ при этом определяется так
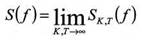
Если U(t) является случайной функцией или суперпозицией случайной и детерминированной функций, то выборочная СПМ является несостоятельной оценкой: дисперсия оценки не зависит от интервала Г, на котором вычисляется выборочная СПМ. Для получения состоятельной оценки используется * метод периодограмм, в котором за оценку СПМ принимают среднее значение ряда выборочных СПМ, вычисленных при разбиении исходной выборки на К секций, т.е.
При конечном числе секций оценка СПМ оказывается случайной величиной при фиксированной частоте fw дисперсия оценки СПМ обратно пропорциональной числу секций К, по которым производится усреднение.
В ходе выполнения задачи студентами исследуется влияние числа секций усреднения на результат вычисления СПМ, влияние формы временного окна на спектр функции, способы увеличить отношение сигнал/шум спектральными методами и другие фундаментальные, но очень функциональные и прикладные свойства спектрального анализа.
Корреляционный анализ
Задача состоит в том, чтобы по реализации x(t) ответить на вопрос: есть ли в реализации периодический сигнал или его нет. Определение формы сигнала не требуется.
Из-за конечной длины выборки N мы всегда имеем дело с оценкой корреляционной функции - случайной величиной, дисперсия которой пропорциональна 1/N. Кроме того, из-за конечной полосы частот шума, оценка автокорреляционной функции Rxx(m) представляет собой функцию с затухающими осцилляциями. Поэтому оценка Rxx(m) помимо осцилляции, обусловленных сигналом, содержит случайную компоненту и затухающие осцилляции, обусловленные шумом. Как показывает
расчет, использование корреляционной функции приводит к увеличению отношения сигнал/шум (S/N).
Дисперсия оценки корреляционной функции обратно пропорциональна длине выборки, а также обратно пропорциональна ширине полосы частот шума (В). Кроме того, дисперсия оценки корреляционной функции зависит от самой корреляционной функции.
Увеличение отношения сигнал/шум (G) в результате вычисления корреляции равно:
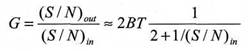
В наиболее интересном для приложений случае, когда (S/N)in<<1, G=2BT(S/N)in.
Описание программного обеспечения
В задаче сбора и анализа данных всегда есть два основных элемента: генератор и приемник (анализатор сигнала). Мы не стали отступать от этого правила и создали три основных виртуальных прибора: генератор нужного нам сигнала и два приемника-анализатора: для спектрального и корреляционного анализа отдельно.
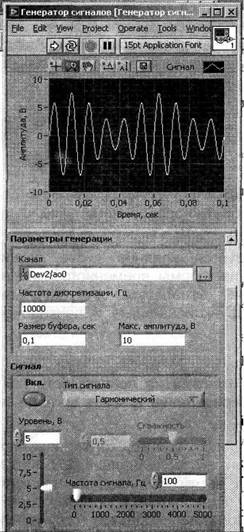
Генерация сигнала
| Элемент управления | Описание |
| Параметры генерации | |
| Канал | Физический канал вывода данных платы (по умолчанию Dev1/ao0. |
| Частота дискретизации | Не должна превышать возможности платы |
| Размер буфера | Период повторения сигнала |
| Макс, амплитуда | Максимальная амплитуда сигнала, не должна превышать возможности платы |
| Сигнал | |
| Тип сигнала | Гармонический, треугольный, прямоугольный, пила |
| Уровень | Амплитуда сигнала, не должна превышать установленную макс, амплитуду |
| Частота сигнала, Гц | |
| Модулятор | |
| Модулируемый параметр | Амплитуда генератора, частота генератора, скважность генератора, амплитуда шума |
| Коэф. модуляции | От 0 до 1. |
| Частота | Частота модуляции |
| Тип функции | Гармоническая, треугольник, прямоугольник |
| Шум | |
| Тип шума | Белый, розовый, узкополосный |
| Амплитуда, В | Амплитуда шума |
| Ширина полосы | Спектральная ширина полосы частот шума |
| Частота, Гц | |
Программа управляет ЦАП платы ввода вывода и позволяет генерировать различные сигналы с заданным пользователем параметрами: частота, форма, наличие одного из трех типов шума, и модуляции.
Корреляционный и спектральный анализ проводятся программами Корреляционный анализатор/Correlation Analyser.exe (КА) и Спектральный анализатор/Spectral Analyser.exe (СА) соответственно. Для работы с обоими программами необходимо соединить выход ЦАП генерации сигнала (аоО по умолчанию) со входом АЦП регистрации (аЮ по умолчанию). Программы одновременно работать не могут.
Окна программ Спектральный и Корреляционный анализатор представлены на рисунке.
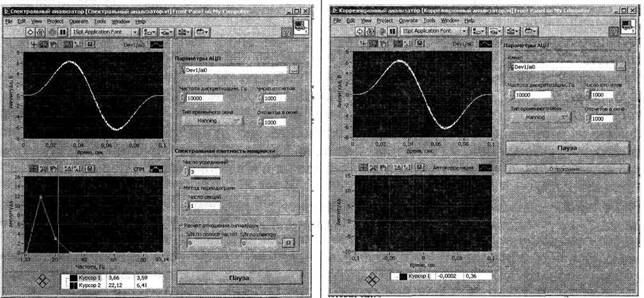
Параметры анализа сигналов приведены в следующей таблице:
| Настройки | Описание |
| Параметры АЦП (общий) | |
| Канал | Канал ввода сигнала |
| Частота дискретизации | |
| Число отсчетов | |
| Тип временного окна | Выбор типа временного окна в выпадающем меню |
| Отсчетов в окне | Ширина окна |
| Пауза (общий) | Приостановить расчет |
| Спектральная плотность мощности (только СА) | |
| Число усреднений | |
| Число секций | Число секций для метода периодограмм |
| S/N по полосе частот | Расчет отношения сигнал/шум |
| S/N по спектру | Расчет отношения сигнал/шум |
Упражнения
| Название | Описание |
| Простейшая иллюстрация эффекта наложения частот. | В этом пункте исследуется спектр гармонического сигнала в зависимости от его частоты и шага дискретизации. |
| Влияние временного окна на разрешение по спектру | Как отмечалось выше, разрешение по спектру определяется длиной временного окна или шириной центрального лепестка спектрального окна. Этот эффект исследуется в данном упражнении. |
| Влияние вида модуляции сигнала на его спектр | Целью этого упражнения является ознакомление со спектром гармонического сигнала, подвергнутого модуляции различного типа. |
| Получение оценки СПМ методом периодограмм | Студенты изучают влияние паарметров метода периодограмм на оценку СПМ |
| Выделение сигнала из шума | Решение основной проблемы задачи: выделение сигнала из шума методом спектрального анализа. |
| Получение оценки корреляционной функции гармонического сигнала | Качественное подавление шума с помощью корреляции |
| Зависимость дисперсии выборочной корреляционной функции от длины выборки. Вычисление эквивалентной полосы частот шума | Рассматривая выборки различной длины, можно проверить связь дисперсии автокорреляционной функции с параметрами ее вычисления. Кроме того, можно вычислить эффективную полосу частот шума. В по экспериментально вычисленной дисперсии шума и дисперсии выборочной корреляционной функции. |
| Выделение сигнала из шума с помощью корреляционной функции Проверка формулы для G | Решение основной проблемы задачи: увеличение отношения сигнал/шум методом корреляционного анализа. |
Выводы
Создана очень удобная в использовании, многофункциональная задача практикума для очень благородной цели: обучение студентов действительно необходимым знаниям и навыкам. Задача выполняется на стандартном оборудовании: плата ввода вывода и персональный компьютер. О возможности использования этих компонент в других приложениях, а не только в данной задаче говорить не приходится. Концепция виртуальных приборов не зря завоевала свою популярность. Что еще можно сказать? Когда я учился, таких не было. Жалко.