Измерительные преобразователи на основе цифровой обработки сигналов предназначены для измерения интегральных характеристик сигналов таких как среднее, средневыпрямленное, среднеквадратичное значения сигналов, определение их спектрального состава, автокорреляционных функций.

Если объект измерения характеризуется двумя или большим числом сигналов, то измерители на основе цифровой обработки сигналов позволяют определить мощность на нагрузке, взаимокорреляционные функции, провести относительные измерения для определения амплитудно-временных характеристик, амплитудно-частотных и фазо-частотных характеристик. Амплитудно-временные и амплитудно-фазо-частотные характеристики являются основой для определения динамических характеристик объекта.

Во всех случаях вышеперечисленных измеряемых величин необходимо вычислять определенный интеграл за некоторый промежуток времени от входного сигнала, умноженного на некоторую вспомогательную функцию.

Для непрерывных сигналов и непрерывных вспомогательных функций эта процедура имеет вид:

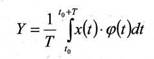
где У- результат измерения, T- время интегрирования, t₀ - начальный момент времени, x(t) - измеряемый сигнал, φ(t) - вспомогательная функция

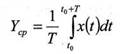
Вспомогательная функция в этом случае тождественно равна единице:

Наиболее распространенными в измерительной технике являются такие характеристики сигнала x(t):

Среднее значение

Средневыпрямленное значение

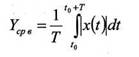
Вспомогательная функция φ(t) = 1 если x(t)>0,

φ(t) = -1 если x(t) < 0. Квадрат среднеквадратического значения

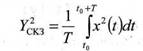
Вспомогательная функция представляет при этом сам сигнал

φ(t) = x(t) Спектральные составляющие сигнала

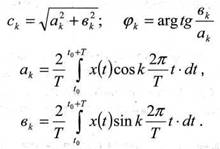
Вспомогательные функции в этом случае

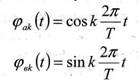
Автокорреляционная функция сигнала

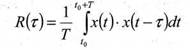
Вспомогательная функция в этом случае

φ(t) = x(t-τ) В тех случаях, когда результат измерения образуется двумя входными сигналами x₁(t) и x₂(t), тоже имеет место интегральное преобразование результата функционального взаимодействия этих двух входных сигналов.

Наиболее распространенными измеряемыми величинами, образованными двумя входными сигналами являются:

Активная мощность

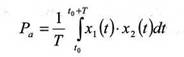
Формула (13) по структуре аналогична формуле (1), если положить x₂(t) = φ(t)

Энергия

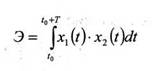
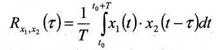
Вспомогательная функция x₂(t) = φ(t)

Взаимокорреляционная функция двух сигналов

Вспомогательная функция x₂ (t-τ) = φ(t)

Как видно из формул во всех перечисленных случаях имеет место интегральное преобразование сигналов на интервале времени Т.

Подинтегральное выражение n(t) представляет собой произведение x(t) и φ(t)

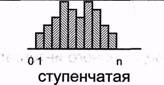
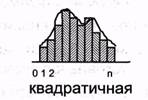
Геометрической интерпретацией определенного интеграла на интервале интегрирования есть площадь, ограниченная подинтегральной кривой и пределами интегрирования.

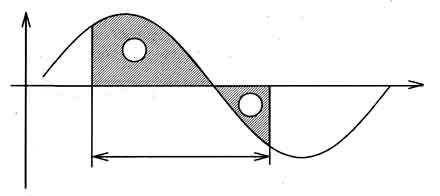
Рисунок 1 - Геометрическая интерпретация определенного интеграла

Причем площади над осью абсцисс приписывается знак "+", а площади под осью абсцисс - знак "-".

Если подинтегральная функция n(t) представлена выборками мгновенных значений n(t_i), полученных через интервалы ∆t_i, то с использованием значений n(t_i) и интервалов ∆t_i. строится аппроксимирующая функция n(t) на интервале Т или несколько аппроксимирующих функций n_j(t) на подинтервале ∆T_j интервала Т, таких, чтобы можно было аналитически вычислить интегральное значение на всем интервале Т или на всех подинтервалах Т_j. интервала Т. В последнем случае интегральное значение на

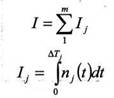
m - количество подинтегралов ∆T_j интервала T находится путем суммирования вычисленных интегралов на подинтервалах ∆T_j интервала T.

Подинтервал ∆T_j может включать несколько интервалов дискретизации ∆t_i

Наиболее распространенной является полиномиальная аппроксимация, когда аппроксимирующий полином проходит через выборочные мгновенные значения. Применяется аппроксимация по методу наименьших квадратов, когда аппроксимирующая функция проходит не через все выборочные мгновенные значения. Аппроксимирующие функции n_j(t) являются финитными, т.е. такими, действие которых ограничено подинтервалами ∆T_j При равномерном шаге дискретизации ∆t_i интегральные значения на участке ∆T_j получаем путем суммирования произведений выборочных значений на весовые коэффициенты, получившие название коэффициентов Ньютона-Котеса. Их значения приведены в [1], а алгоритмы вычисления определенных интегралов после аппроксимации выборочных значений полиномами 0-го, 1-го, 2-го и 3-го порядков представлены в табл. 1.

Таблица 1 - Алгоритмы вычисления среднего интеграла на интервале 0 - n при различных видах кусочно-полиномиальной аппроксимации

Вид аппроксимации	Порядок полинома	Алгоритм вычисления среднего на интервале 0 –n R - остаточный член j-го участка
	0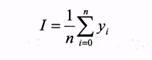
	1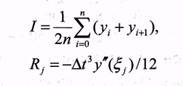
	2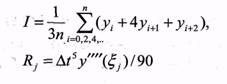
	3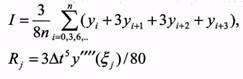

Кроме аппроксимации финитными функциями применяют аппроксимацию так называемыми восстанавливающими вспомогательными

функциями, вид которых не зависит от количества выборочных значений. Самой распространенной восстанавливающей вспомогательной функцией является функция отсчетов

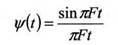
Для сигналов с ограниченным спектром в соответствии с теоремой Ф.А.Котельникова подинтегральное выражение n(t) может быть полностью восстановлено по выборочным значениям в соответствии с формулой (22), если частота дискретизации не менее чем в 2 раза выше наивысшей спектральной составляющей подинтегральной функции

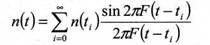
где F - частота дискретизации, а число выборочных значений стремиться к бесконечности.

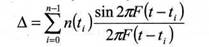
Определенный интеграл вычисляется по формуле

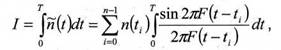
Если количество выборочных значений ограничено, то восстановление подинтегральной функции и соответственно интегрального значения происходит приближенно, т.е. с некоторой погрешностью.

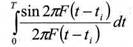
где n(t) - восстановленная подинтегральная функция при ограниченном числе выборочных значений.

Выражение представляет собой интегральный синус, для которого отсутствует первообразная в аналитической форме и он может вычисляться численно или задается таблично. Поэтому программное обеспечение проектируемого преобразователя должно содержать или программу вычислений или массив значений интегрального синуса для заданного числа n выборочных значений.

Исходя из условий минимизации погрешности интегрирования интегральное значение подинтегральной функции вычисляется по формуле

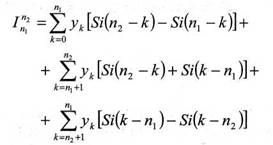
где n(t_k) - к-ое выборочное значение подинтегральной функции,

Si(n₂ -к) - значение интегрального синуса от аргумента ∆t(n₂ -к),

∆t –интервал дискретизации.

Соотношение частоты сигнала и частоты дискретизации

Соотношение частоты сигнала и частоты дискретизации зависит от вида аппроксимации и вида подинтегральной функции.

Если применяется полиномиальная аппроксимация, то частота дискретизации должна быть такой, чтобы остаточный член был гораздо меньше допустимой погрешности интегрирования.

Максимальное соотношение частоты высшей гармоники сигнала и частоты дискретизации при аппроксимации восстанавливающей вспомогательной функцией Котельникова, как известно равно 0.5. Но очень важно помнить, что это соотношение должно распространяться не только на частоту сигнала, но и обязательно на частоту подинтегрального выражения, представляющего собой произведение сигнала на вспомогательную функцию.

Например, при измерении среднего напряжения синусоидального сигнала вспомогательная функция равна 1 и допустимое соотношение частоты сигнала и частоты дискретизации равно 0.5. При измерении квадрата эффективного напряжения вспомогательная функция φ(t) равна x(t) и, если входной сигнал синусоидальный, то в подинтегральном выражении появляется

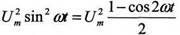
вторая гармоника т.к. и частота дискретизации должна быть в четыре раза больше, чем частота сигнала.

В анализаторах спектра вспомогательная функция равна sin kωt или соs kωt. Произведением высшей k-ой гармоники сигнала и ее вспомогательной функции sin kωt также образуется вторая гармоника

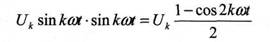
с частотой 2kω и частота дискретизации должна быть больше чем 4kω.

Таким образом, при необходимости цифровой обработки в диапазоне частот до 100 кГц необходимо применять АЦП с частотой дискретизации не менее 400 кГц.

В выражениях числовые характеристики переменного напряжения представляют собой усредненный интеграл на интервале интегрирования Т

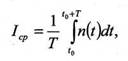
откуда видно, что для периодических сигналов адекватный результаты получают, если интервал интегрирования равен или кратен периоду подинтегральной функции. Только в этом случае будет выделена постоянная составляющая или отфильтрована (среднее значение равно нулю) переменная составляющая. При этом лучше, если интервал интегрирования Г кратен интервалу дискретизации ∆t. В противном случае необходимо строить канал для точного определения периодами частоты сигнала или определять момент перехода через ноль по двум рядом расположенным выборочным значениям с разными знаками путем линейной интерполяции.

Исходя из выше описанного построена функциональная схема измерительного преобразователя на основе цифровой обработки сигналов с использованием процессора и карты фирмы National Instruments в среде LabVIEW (рис. 2).

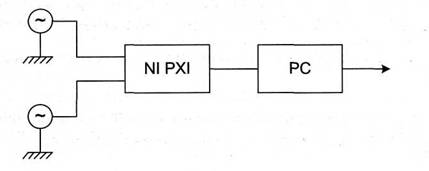
Рисунок 2 - Функциональная схема измерительного преобразователя на основе цифровой обработки сигналов с использованием процессора и карты фирмы National Instruments в среде LabVIEW

Если частота дискретизации ниже частоты сигнала, в восстановленном сигнале с применением функции Котельникова образуются частоты, представляющие собой дробную часть отношения частоты сигнала и частоты дискретизации.

Докажем это.

Пусть входной сигнал полигармонический

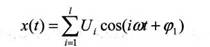
Частота дискретизации

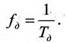
Обозначим отношение частоты сигнала и частоты дискретизации

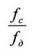
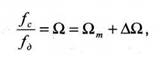
где Ω_M= INT(Ω) и ∆Ω - целая и дробная части отношения соответственно.

Подставив получим выборочные значения сигнала

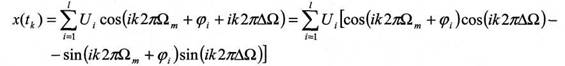
С учетом периодичности тригонометрических функций, получим

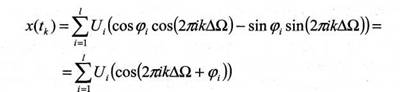
Следует, что выборочные значения полигармонического сигнала переносятся на частоту дробной части ∆Ω, отношения частоты сигнала и частоты дискретизации, и каждая составляющая при восстановлении с использованием функции Котельникова будет восстановлена на этой относительной частоте.

Частота составляющих восстановленного сигнала находится по формуле

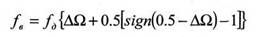
Для 0,5< Ω <1 фаза сигнала меняется на 180°, т.к. абстрактное понятие отрицательной частоты адекватно сигналу той же частоты, однако находится в противофазе.

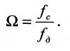
На рис. 3 представлена зависимость относительной частоты восстановленного сигнала от относительной частоты

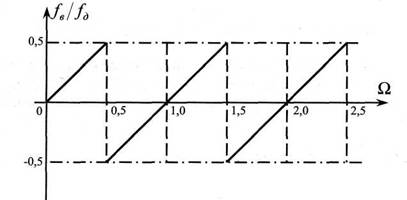
Рисунок 3 - Зависимость относительной частоты восстановленного сигнала от частоты сигнала

Использованная литература

1 Г.Корн, Т.Корн. Справочник по математике. Для научных работников и инженеров. М., 1977, 832 стр. с илл.

..............................................................................................................................