1. Постановка задачи

В настоящее время инструментальные системы графического моделирования динамических систем (Simulink, Simulation Module, SystemBuild) стали широко использоваться для модельного проектирования встраиваемых управляемых систем. Ориентация на создание прототипа реальной системы предъявляет к таким пакетам ряд новых требований. Одним из наиболее важных - является требование к быстродействию и необходимой точности методов численного интегрирования (решателей) с фиксированным шагом. Пакеты используют классические методы различных порядков точности. Точные методы интегрирования (Рунге-Кутта 4, Адамса-Башфорта и др.) требуют значительных временных затрат для получения решения. Одним из показателей эффективности метода принято считать количество вычислений правой части дифференциальных уравнений. По этому показателю метод Рунге- Кутта 4 уступает методам прогноза-коррекции, к которым относится метод Адамса-Башфорта. Существенным недостатком последнего является необходимость выполнения так называемого «участка разгона» с применением другого численного метода. Использование прототипа объекта управления или контроллера в петле с реальной аппаратурой (HIL) предъявляют к численному методу интегрирования, реализуемому на целевом микропроцессоре выполнения дополнительных требований:

-возможность распараллеливания процесса вычислений;

-обеспечение необходимой точности получения решений в заданном частотном диапазоне при известной длине машинного слова целевого микропроцессора;

-минимальные аппаратурные затраты для выполнения арифметических операций;

-минимальный объем регистрового запоминающего устройства;

-автоматическая настройка структуры прототипа;

-алгоритм управления прототипом не должен приводить к усложнению процесса моделирования в целом;

-автоматическая генерация исполняемого кода.

Перечисленные выше требования имеют противоречивый характер в силу специфических свойств методов численного интегрирования. Более высокий порядок точности метода обеспечивает заданную погрешность при большем шаге интегрирования. Это приводит к тому, что на одинаковом промежутке интегрирования точные методы обеспечивают меньшее число шагов интегрирования, но при этом необходимо выполнять больший объем вычислений. Зависимость между точностью метода и числом шагов интегрирования справедлива только для достаточно больших значений шага интегрирования. При малых значениях шага (lim h=0) практически все используемые методы численного интегрирования становятся эквивалентными методу Эйлера. Это утверждение доказывается тем, что в разностных уравнениях значения производных становятся практически равными. В результате несложных преобразований получается разностное уравнение для метода Эйлера. Малое значение шага достижимо на современной микропроцессорной 6aзe (DSP, FPGA и FPOA). Одновременное выполнение базовой операции вычисления суммы произведений (MAC) выполняется за один машинный такт равный 10^-8 сек.

Инструментальные пакеты моделирования устанавливаются на однопроцессорных компьютерах. Создания прототипа динамической системы, работающего в натуральном масштабе времени, возможно, только на высокоскоростных вычислительных системах. Стоимость таких систем будет определять и стоимость выполнения полного цикла модельного проектирования встраиваемых систем управления. Более эффективным является вариант построения прототипа с помощью многопроцессорной системы, выполняющей параллельную реализацию численного интегрирования. Задачи численного интегрирования обыкновенных дифференциальных уравнений не относятся к классу задач с естественным параллелизмом. Варианты распараллеливания вычислений правых частей уравнений сильно зависят от вида уравнений. Теоретические аспекты построения моделирующих микропроцессорных систем впервые рассмотрены в работе [1]. Автор детально описывает различные варианты МП-структур для параллельного моделирования систем обыкновенных дифференциальных уравнений, представленных в нормальной форме Коши. Процесс распараллеливания базируется на нахождении оптимального расписания. Составление оптимального расписания работы процессоров является достаточно сложной задачей, требующей выполнения целого ряда жестких требований. Из условия оптимальности расписания необходимое число процессоров должно соответствовать количеству узлов дерева, принадлежащих одному уровню и времена обработки узлов (вычислительных функций) должны быть одинаковыми. Если эти времена не одинаковы, что чаще всего бывает на практике, то при составлении расписания в случае использования рассмотренного алгоритма возникают неожиданные эффекты. Перед началом моделирования в программную часть каждого микропроцессора (МП) загружаются программы работы тех решающих блоков (РБ), функции которых данный МП выполняет в цикле интегрирования в соответствии предварительно составленным расписанием. Уменьшение времени вычисления правых частей уравнений за счет значительного числа РБ приводит к увеличению времени обмена информацией между ними. Процесс обмена информацией не возможно реализовать параллельно из-за сложности устройства коммутации. При этом теряется производительность моделирующей системы в целом. Значительный промежуток времени основным средством моделирования являлись различные аналоговые устройства и машины. В настоящее время в силу целого ряда объективных причин происходит дальнейшее развитие аналоговых принципов моделирования с использованием неаналоговой формы представления информации.

Направление, связанное с использованием микропроцессоров в моделирующих системах, позволяет создать широкий спектр средств моделирования, которые равномерно покрывают область «быстродействие - точность». МП системы моделирования [1] отличаются от АВМ дискретным представлением информации и программным управлением функциями решающих блоков (РБ) и связями между ними. Нежелательные последствия неизбежной в данном случае дискретизации непрерывного объекта моделирования могут свести к минимуму потенциальные преимущества таких систем. В связи с этим математический и структурный аспекты моделирования непрерывных процессов нуждаются в тщательном анализе. Например, совершенно очевидно, что точность и быстродействие МП-систем находятся в прямой связи с распределением функций между РБ и выбором того или иного метода численного интегрирования.

В работе [2] исследованы математические методы и разработаны на их основе принципы построения последовательно-параллельных интегрирующих структур, предназначенных для моделирования динамических систем в реальном масштабе времени. В основе аппаратной реализации интегрирующих структур лежит вариант построения автоматизированного аналогового процессора [3,4]. Структурная схема процессора, реализующего систему неоднородных дифференциальных уравнений третьего порядка

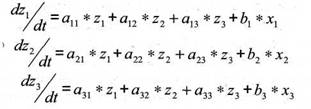
представлена на рис.1. Такая структура соответствует дискретной аппроксимации непрерывной системы и является примером несинхронной импульсной системы. Ключевые элементы перед каждым из интеграторов работают с одинаковой частотой, но несинхронные по фазе. Несинхронное прерывание, выполняемое ключевыми элементами, является свойством структуры процессора, реализующего численных метод интегрирования. Метод, описанный в работах [2,5], является новой модификацией метода Эйлера. При выполнении определенной коррекции метод становится практически тождественным по точности методам второго порядка.

Число интеграторов (рис.1) совпадает с классическим способом реализации на АВМ. Отличительной особенностью вычислительного процесса является последовательный принцип интегрирования правых частей заданных уравнений, не требующий одновременного существования всех связей между интеграторами. Последовательный принцип работы интеграторов определил название нового численного метода (МПИ). Необходимые связи между интеграторами осуществляются за счет одновременного срабатывания пар ключевых элементов, стоящих во входных и выходных цепях. Кроме выполнения арифметических операций, представленных в разностных уравнениях на рис.1, интеграторы обеспечивают и хранение промежуточных значений выходных переменных. Время срабатывания ключевых элементов указано для первого цикла определения переменных z_1,i; z_2,i; z_3,i . Для последующих циклов последовательность срабатывания ключей не изменяется.

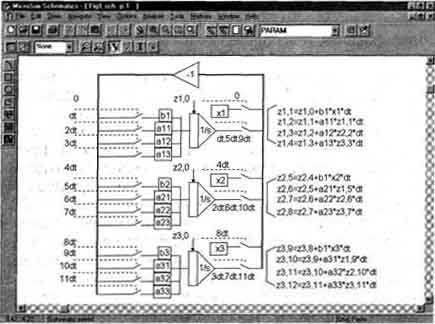
Рис.1 Структурная схема аналогового процессора

Разработка такого варианта реализации была предпринята в связи с необходимостью создания полностью автоматизированного аналогового процессора с минимальными аппаратными затратами на создание системы автоматической коммутации (САК) операционных блоков и на установку коэффициентов передачи с помощью умножающих цифро-аналоговых преобразователей ЦАП(ОАС).

Инструментальные системы графического моделирования динамических систем (Simulink, Simulation Module, SystemBuild) является уникальными средами для исследования подобных динамических систем. Они позволяют моделировать работу рассмотренной выше интегрирующей структуры и произвести анализ методической ошибки, возникающей за счет интегрирования импульсно-модулированных сигналов.

2. Описание решения

Первая часть статьи посвящена доказательству работоспособности автоматизированного аналогового процессора путем создания вариантов моделей в перечисленных выше инструментальных системах и сравнения их возможности и эффективности.

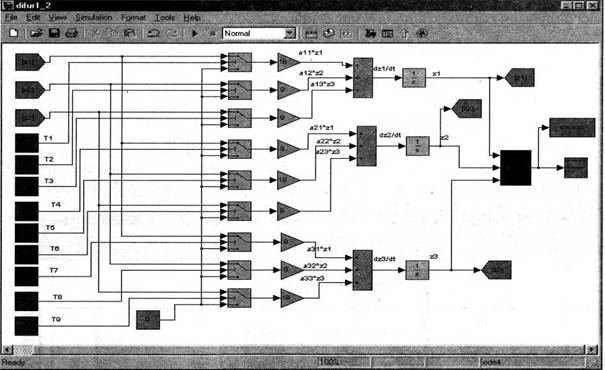
Рис.2 S-модель difur1_2.mdl

Первый вариант S-модели процессора создан для детального понимания принципа его работы. Модель (файл difur1_2.mdl) представлена на рис.2. Она реализует решение однородной системы уравнений, что требует внесения определенных изменений в схему аналогового процессора. Необходимо исключить разностные уравнения с переменными х₁,х₂,х₃. и убрать соответствующие ключевые элементы. В модели используются стандартные функциональные блоки Simulink Library. Для реализации сумматора- интегратора используются сумматор с тремя входами и одновходовой интегратор. Функции ключевых элементов выполняют блоки Switch из раздела библиотеки Signal Routing. Установка значений постоянных коэффициентов a_y выполнение операций умножения на зависимые переменные z_i обеспечивается решающими блоками Gain. Для задания требуемой последовательности срабатывания ключевых элементов и времени их замкнутого состояния используются генераторы прямоугольных импульсов Pulse Generator в режиме работы Sample based. Для обеспечения максимальной точности интеграторов выбран Solver ode5 (Dormand-Prince). Значение фиксированного шага совпадает со временем замкнутого состояния ключевых элементов и равно 0.001s. Полученные в результате моделирования решения z1(t),z2(t),z3(t) выводятся на виртуальный осциллограф Scope и в рабочую область Workspace. Отсутствие ключевых элементов на выходах интеграторов отличает эту модель от схемы рис.1., но принципиально не изменяет ее функционирование.

Второй вариант S-модели и аналоговый процессор (рис.1) имеют практически одинаковые структуры. В модели реализована общая шина. Для этого в модель включены блоки IvTux и Demux. С целью приближения к аппаратной реализации[4] входные и выходные ключи, генераторы управляющих импульсов объединены в соответствующие модули Input Switch,Output Switch,Control Inp и Control Out. Модули в модели представлены подсистемами, хранящимися в файлах Unit_switch_lnp.mdl, Unit_switch_Out.mdl, Unitcontrolinp.mdl, Unit_control_put.mdl. Число блоков Gain сокращено с девяти до трех. Каждый из блоков выполняет операции поэлементного умножения векторов [а₁₁ а₁₂ a₁₃].*[z₁ z₂ z₃].[a₂₁ а₂₂ a₂₃].*[z₁ z₂ z₃],[a₃₁ a₃₂ a₃₃].*[z₁ z₂ z₃].

S-модель (файл difur1_3m.mdl) представлена на рис.3. Для оценки погрешности полученного решения переменной z_i(t) производится формирование известного аналитического решения z_i(t) = -2·e^t + е^4t с помощью блоков Ramp и Matlab Fen. Исследуемая система задана уравнениями:

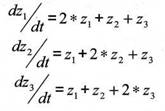
и имеет следующие начальные условия z₁(0)=-1, z₂(0)= z₃(0)=2.

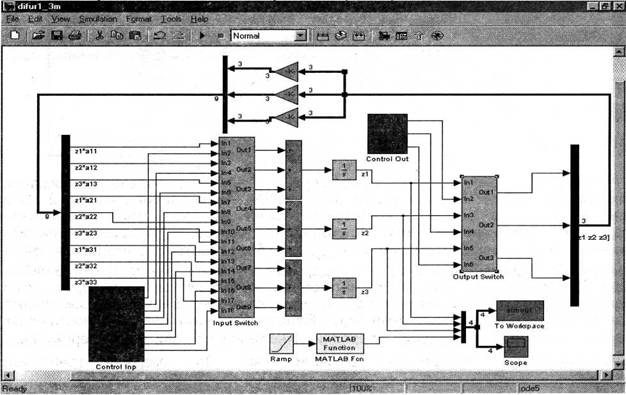
Рис.3 S-модель difur1_3m.mdl

Для устранения одной из составляющих методической погрешности МПИ[2] коэффициенты исходного уравнения необходимо увеличить в девять раз. Это достигается установкой соответствующих параметров блоков Gain.

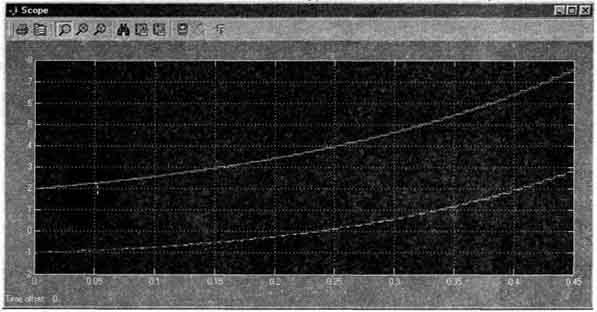
Рис.4 Графики решений системы уравнений

Графики полученных решений системы уравнений показаны на рис.4.

Пакет моделирования Simulation Module практически обладает такими же возможностями по сравнению с Simulink. Модель системы может быть создана непосредственно в среде LabVIEW. Представленная на рис.5 модель системы, получена в результате трансляции S-модели с проведенными изменениями настроек свойств блоков Switch, Pulse Generator и параметров выполнения моделирования (Configure Simulation Parameters). В списке решателей дифференциальных уравнений отсутствует метод ode5 (Dormand-Prince) и пришлось использовать метод Рунге-Кутта 4.

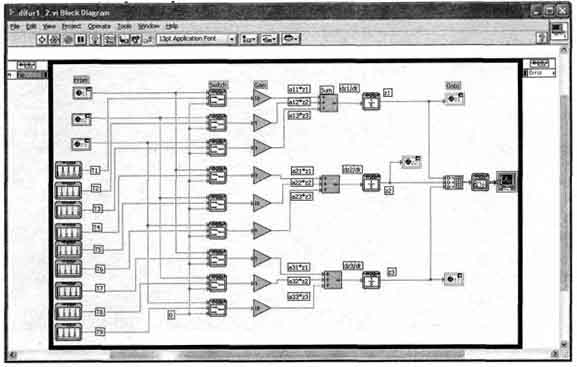
Рис.5 VI -модель difuri 2.vi

Второй вариант реализации S-модели difur1_3m.mdl(pnc.3) не может быть оттранслирован в соответствующую Vl-модель. Транслятор не обеспечивает корректную адекватную замену иерархических моделей Simulink, что значительно сужает класс моделей. На рис.6 представлен вариант построения модели с шинной организацией. В нижней части рисунка изображен узел Matlab Script Node, осуществляющий воспроизведение аналитического решения первого уравнения системы. Необходимо отметить, что обращение к ядру Matlab из тела цикла Simulation Loop значительно увеличивает время реализации модели. В дальнейших исследованиях аналитические решения воспроизводились с помощью функциональных блоков LabVIEW из библиотеки Mathematics.

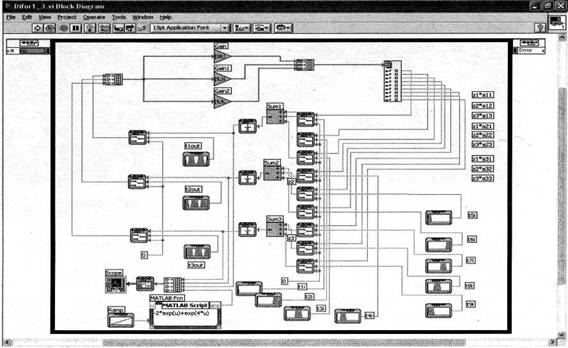
Рис.6. Модифицированная Vl-модель системы

Результаты моделирования тестовой системы уравнений представлены на рис.7.

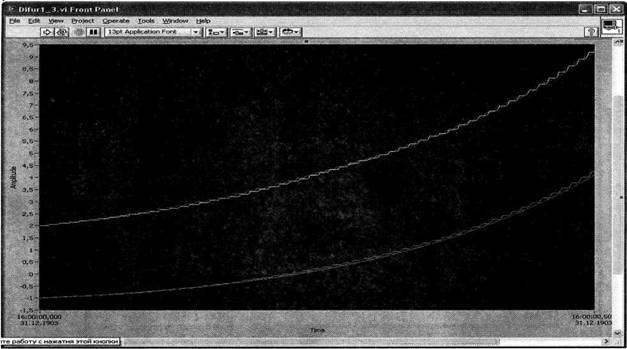
Рис.7. Осциллограммы решений на Vl-модели системы

Оценка погрешности результатов моделирования производилась за счет сравнения с известными аналитическими решениями, а также с решениями, полученными при использовании встроенного в Simulink редактора дифференциальных уравнений DEE. Реализация непрерывной модели системы третьего порядка была произведена в пакете SystemBuild с целью сравнения возможностей трех инструментальных систем моделирования.

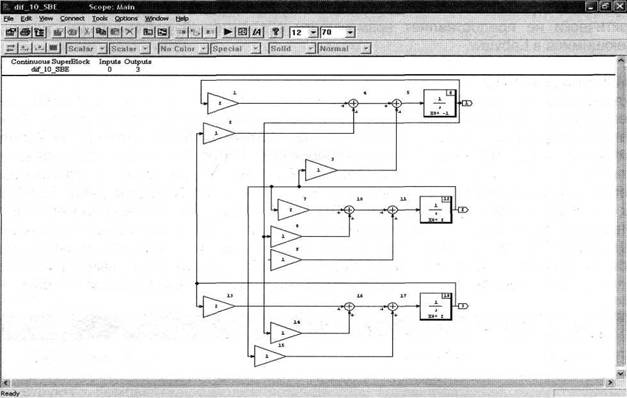
Рис.8. Модель непрерывной тестовой системы

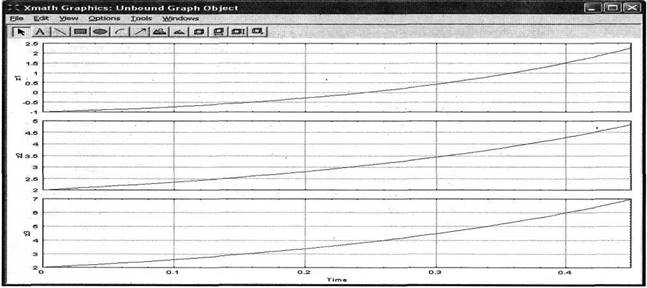
Рис.9. Графики решений в SystemBuild

При работе с моделями было необходимо подтвердить теоретически полученные способы коррекции методической погрешности предложенного численного метода. Достичь необходимого значения частоты срабатывания ключевых элементов (шага интегрирования) не удалось по следующим причинам. При частоте срабатывания ключей большей 10 кГц наблюдается неустойчивость их работы. Начиная со значения шага интегрирования h=10^-4 сек виртуальные осциллографы Scope и SimTime Waveform из-за ограниченного объема памяти буфера не обеспечивают непрерывного наблюдения графиков решений на всем промежутке интегрирования. Этот существенный недостаток преодолим в Simulink за счет возможности передачи результатов моделирования в рабочее пространство Workspace и их дальнейшей обработки средствами Matlab. Такой же прием визуализации решений применим и в пакете SystemBuild. Структура Simulation Loop практически не предоставляет возможности эффективной работы с массивами, имеющимися в LabVIEW.

3. Используемое ПО

Включенные в состав всех рассмотренных модулей точные решатели не обеспечивают исследование моделей в натуральном масштабе времени. При времени переходного процесса исследуемой системы 0,45 сек модельное время при наибольшем значении шага интегрирования h=10^-3 секунды составляет в Simulink 5 сек, а в Simulation Module 8,5 сек. Отчет работы программы профилировщика LabVIEW представлен на рис.10. Величина Total Time равна 98,6719 сек при шаге интегрирования равным 10^-4 сек. Исследование поведения моделей с меньшими значениями шага интегрирования при таких скоростях получения решений не имеет смысла. При малом значении шага начинают проявляться инструментальные погрешности, обусловленные алгоритмами вычислений и длинной машинного слова при представлении числовых данных в формате double.

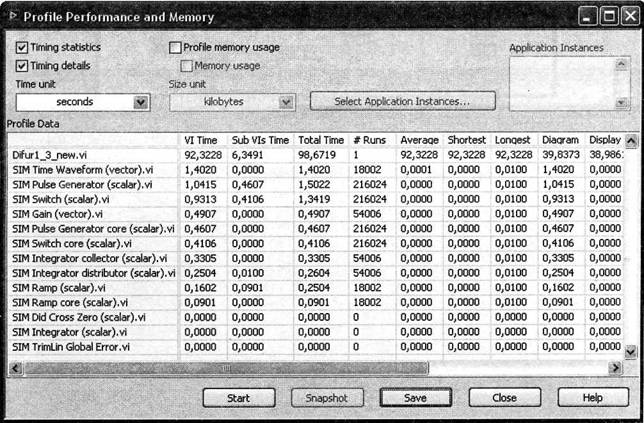
Рис.10 Отчет программы Profile 4.

Развитие решения

1. Результаты проведенного исследования подтверждают теоретические выводы

2. Доказана возможность реализации автоматизированного аналогового процессора

3. Проведенный анализ погрешности показал, что точность метода МПИ выше, чем у метода odei(Euler) и практически совпадает с методом ode2(Heun)

4. Решение тестового уравнения не может быть получено в реальном времени (за 0,45s) во всех системах моделирования _;

5. Низкая скорость моделирования подтверждает необходимость аппаратной реализации решателей ОДУ.

Список литературы

1. Р.Е. Танкелевич Моделирующие микропроцессорные системы. М: Энергия, 1979,120 с.

2. К.Г. Жуков Методы и средства реализации последовательно-параллельных интегрирующих структур. Автореферат диссертации на соискание ученой степени к.т.н., Ленинград, 1988.

3. К.Г. Жуков, В.И Проскуряков. Устройство для коммутации задач на аналоговых вычислительных машинах. А.С. 888138 (СССР). Опубл. в Б.И., 1981, № 45.

4. К.Г. Жуков, Е.А. Лоренц Специализированный аналоговый процессор на линейных интегральных схемах. В сб.: Линейные интегральные схемы и их применение в приборостроении и промышленной автоматике. Тезисы докладов Всесоюзной научно-технической конференции. Ленинград, 1977.

5. К.Г Жуков, М.В. Подобед. Модифицированный метод Эйлера и его реализация средствами АЦВТ. В сб.: Теория и методы построения импульсных вычислительных устройств. Труды расширенного заседания Международной ассоциации по аналоговым вычислениям. Рязань, 1978.

6. К.Г. Жуков Моделирование последовательно-параллельных интегрирующих структур. Компьютерное моделирование 2002:Труды Междунар. Науч.-техн. конф. СПб.: Изд-во СПбГПУ, 2002,230 стр.

7. К.Г. Жуков Применение пакета Fixed-Point Blockset в разработке устройств,,-. реального времени. Тезисы докладов Всероссийской научн. конф.

«Проектирование научных и инженерных приложений в среде MATLAB», М.: ИПУ РАН, 2004.

8. К.Г. Жуков Возможности LabVIEW в модель-ориентированном проектировании встраиваемых систем управления. Материалы международной конф. «Образовательные, научные и инженерные приложения в среде LabVIEW и технологии National Instruments», M.:, РУДН, 2005.

9. К.Г. Жуков Новые возможности LabVIEW в проектировании систем управления. Материалы международной конф. «Образовательные, научные и инженерные приложения в среде LabVIEW и технологии National Instruments», M.:, РУДН, 2006.