В работе предлагаются методы расширения полосы пропускания стробоскопических осциллографов за счет априорной информации об их характеристиках. С помощью среды LabVIEW и интерфейсной платы GPIB-USB-B проводится математическое моделирование прохождения сигналов через стробоскопический осциллограф, исследование и апробация методов расширения полосы пропускания.

Введение.

Основным направлением развития импульсных и цифровых устройств всегда было увеличение быстродействия и пропускной способности каналов передачи. Очевидно, что это достигается путем уменьшения длительности и периода следования сигналов, т.е. увеличения частотного диапазона. К настоящему времени освоен диапазон длительностей порядка 2-10"¹² с. Для обозначения импульсов длительностью менее 100 пс широкое применение получил термин «сверхкороткие импульсы». Сверхкороткие импульсы принадлежат к классу сверхширокополосных (СШП) сигналов. Оказалось также, что повторяющиеся импульсы подобной длительности обладают рядом специфических свойств, позволяющих использовать их для решения новых задач, недоступных для обычной радиотехники.

На использовании сверхкоротких импульсов основывается новый чрезвычайно перспективный раздел прикладной радиоэлектроники, обозначаемый в англоязычной литературе термином "Ultra-Wide Band (UWB), Short-Pulse Electronics" - радиоэлектроника коротких СШП импульсов. В настоящее время более 250 ведущих мировых фирм и исследовательских центров занимаются разработкой технологий и радиотехнических средств на основе использования сверхкоротких импульсов, в основном это технологии СШП радиолокации и СШП радиосвязи.

Кроме этого в данной области науки ведутся активные и широкомасштабные исследования по следующим направлениям: имитация быстропротекающих процессов в современных ядерно-физических установках, разработка оружия на новых физических принципах, противодействие электромагнитному терроризму, микромощная радиолокация в медицине, подповерхностная георадиолокация.

Наиболее полно актуальность и перспективы развития новых технологий на основе сверхкоротких импульсов раскрывает следующий факт -предполагающееся внедрение СШП технологий в промышленности сравнивается экспертами по возможным последствиям с внедрением полупроводниковых приборов.

Одной из важнейших проблем при проведении исследовательских и опытно-конструкторских работ по созданию перспективных быстродействующих импульсных и цифровых систем является отсутствие регистраторов и средств измерений параметров сверхкоротких импульсов.

Лучшие образцы современных зарубежных стробоскопических осциллографов позволяют измерять импульсные сигналы длительностью порядка 2,5 пс, т.е. в полосе частот до 140 ГГц. Достигнутый отечественный уровень в этой области приборостроения

- до 26 ГГц при использовании отечественной элементной базы,

- до 40 - 60 ГГц при использовании покупной элементной базы.

При этом возникает замкнутый круг - отставание в технологиях производства быстродействующей электронно-компонентной базы ограничивает ширину полосы пропускания создаваемых средств измерений, а отсутствие сверхширокополосных средств измерений ограничивает возможности по созданию высокопроизводительных и высокоскоростных устройств и интегральных схем.

В качестве одного из способов решения данной проблемы предлагается создание методов «искусственного» расширения полосы пропускания средств измерений за счет априорной, прецизионно определенной информации об их характеристиках. В данной статье будут рассмотрены два метода - метод восстановления во временной области формы входного сигнала по известной импульсной характеристике и метод восстановления в частотной области формы входного сигнала по известной амплитудно-частотной характеристике. Предлагаемый методический аппарат предполагается реализовать программно с помощью метода многопараметрической регуляризации, так как на практике из-за погрешностей измерений обратная задача восстановления сигнала (приведения сигнала ко входу) некорректна по Адамару [2].

Вследствие значительных требований к производительности вычислительных устройств ранее не проводились теоретические и экспериментальные исследования реализуемости данного подхода. В результате создания регистраторов и средств измерений параметров сверхкоротких импульсов, а в дальнейшем системы метрологического обеспечения, откроются новые возможности развития перспективных направлений во многих областях науки и техники.

Постановка задачи.

Применительно к данной задаче, стробоскопический осциллограф можно представить как линейное динамическое звено (систему), характеризуемую следующим свойством: его выходной сигнал определяется не только величиной входного сигнала в рассматриваемый момент времени, но и «предысторией» этого сигнала. Динамическая система, иначе говоря, обладает конечной или бесконечной памятью, от которой зависят особенности преобразования входного сигнала.

При решении задач о прохождении разнообразных сигналов через сверхширокополосные динамические системы чаще всего прибегают к временному представлению свойств сигналов и систем (динамическому представлению). Это обусловлено тем, что первичной измерительной информацией является форма сигнала во времени. При дальнейшей обработке применим, а иногда и более удобен анализ в частотной области, когда сигналы задаются рядами или интегралами Фурье.

В первом случае свойства смесителя полностью описываются импульсной характеристикой h(t), являющейся откликом на входной сигнал в виде дельта функции S(t). Зная импульсную характеристику линейной стационарной системы, можно формально решить любую задачу о прохождении сигнала через такую систему. Выходной сигнал представляет собой свертку двух функций - входного сигнала и импульсной характеристики системы. Операция свертки описывается формулой (1), которую также называют интегралом Дюамеля:

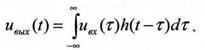
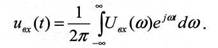
А также если известен частотный коэффициент передачи K(jω) системы, то имеем представление выходного сигнала:

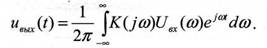
Говоря о спектральном методе анализа прохождения сигналов через линейную систему, имеют в виду использование свойств частотного коэффициента передачи. Если на выходе смесителя действует детерминированный сигнал u_вх(t), который задан обратным преобразованием Фурье:

Данная основная формула спектрального метода свидетельствует о том, что частотный коэффициент передачи системы служит множителем пропорциональности между спектральными плотностями сигналов на входе и выходе:

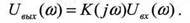
Таким образом отличительная черта анализа в частотной области -эффект преобразования сигнала в системе отображается просто алгебраической операцией умножения.

Спектральный и временной подходы полностью эквивалентны друг другу. Интеграл Дюамеля (1), является сверткой функций во временной области, значит спектральная плотность выходного сигнала (4) есть произведение спектральных плотностей функций u_вх(t) и h(t).

Рис. 1 - Предпосылки методического аппарата восстановления формы входных сигналов

Математическое моделирование прохождения сигналов через сверхширокополосный стробоскопический смеситель.

Восстановление формы входных сигналов является обратной задачей, в которой по известным выходному сигналу и характеристике системы, необходимо определить входное воздействие. В теории радиотехнических цепей эту задачу принято называть приведением сигнала ко входу. С практической точки зрения вызывает интерес только возможность восстановления широкополосного сигнала, прошедшего через заведомо менее широкополосную цепь, т.е. искаженного. Применительно к самой цепи эту процедуру можно рассматривать как расширение ее полосы пропускания.

В качестве воздействующих входных сигналов будем использовать гармонический, треугольный, пилообразный и импульсный сигнал, которые представим как дискретную последовательность (x₀, x₁,...x_N-1) отсчетов во времени, с известным интервалом (шагом) дискретизации ∆ = t₁ –t₀ = t₂ –t₁= ..., где N - конечное количество отсчетов, на котором будет задаваться целое количество периодов сигнала.

Произведение N∆ определяет размер временного окна измерителя стробоскопического.

Одновременно с каждым отсчетом полезного сигнала на смеситель воздействует отсчет псевдослучайной последовательности, распределенной по нормальному закону:

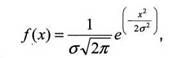
с математическим ожиданием равным нулю и среднеквадратическим отклонением σ.

В качестве характеристик сверхширокополосного стробоскопического смесителя используются близкие к ним характеристики физически реализуемых фильтров нижних частот. Используется два вида фильтров.

Фильтр с максимально-плоской характеристикой или фильтр Баттерворта, коэффициент передачи по мощности которого:

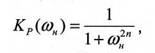
где ω_н = ω/ω_c - безразмерная нормированная частота;

ω_c - частота среза;

n - порядок фильтра.

А также фильтр Чебышева, коэффициент передачи по мощности которого задается формулой:

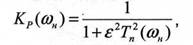
где ε ≤ 1 - коэффициент неравномерности характеристики в полосе пропускания;

Т_n(ω_н) - многочлен Чебышева n - го порядка, определяемый выражением Т_n(х) = cos(n arccos x).

При представлении во временной области дополнительно вводится последовательность длинной N отсчетов, первый элемент которой равен единице, а все остальные нулю. При прохождении данной последовательности через фильтр выходной сигнал является по определению импульсной характеристикой фильтра.

Поскольку в действительности частотный коэффициент передачи (или импульсная характеристика) стробоскопического смесителя будет определен с погрешностью, значения коэффициента передачи суммируются с заданной систематической и случайной (распределенной по нормальному закону (5)) погрешностью измерения.

Если количество отсчетов невелико (до 4096), то выходной сигнал рассчитывается непосредственно во временной области по формуле (1), представленной для дискретных сигналов как ряд:

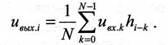
При большем количестве отсчетов целесообразно сначала выполнить преобразование Фурье входного сигнала, затем произведение полученных коэффициентов на отсчеты частотного коэффициента передачи, и перейти обратно во временную область путем обратного преобразования Фурье полученной спектральной плотности выходного сигнала:

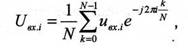
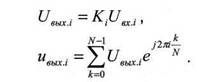
Такой способ вычисления более экономичен, чем прямое использование формулы (8).

Для еще более близкого приближения модели к физике смесителя найденный выходной сигнал суммируется со случайной последовательностью, имитирующей собственные шумы смесителя.

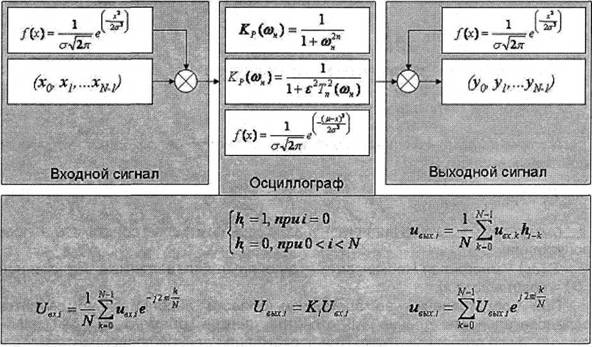
Рис. 2 - Обобщенная структурная схема математической модели прохождения сигналов через сверхширокополосный стробоскопический осциллограф

Описание решения.

Математическое моделирование прохождения сигналов через сверхширокополосный стробоскопический осциллограф, а также метод восстановления во временной области путем решения уравнения обратной свертки и метод восстановления в частотной области путем деления на частотный коэффициент передачи (метод инверсного фильтра) были реализованы программно в среде LabVIEW 8.0. На рис. 2 представлена обобщенная структурная схема модели, на рис. 3 - внешний вид управляющего окна программы.

Для большей наглядности получаемых результатов при восстановлении сигналов в частотной области выполнялось обратное преобразование Фурье для наблюдения во временной области. При исследовании учитывались реальные характеристики стробоскопических измерителей, такие как среднее квадратическое значение собственных шумов 2,5 мВ, количество отсчетов во временном окне 256 - 4096. Поскольку в действительности частотный коэффициент передачи (или импульсная характеристика) стробоскопического осциллографа будет определен с погрешностью, значения коэффициента передачи суммируются с заданной систематической и случайной (распределенной по нормальному закону) погрешностью измерения. Для еще более близкого приближения модели к физике смесителя найденный выходной сигнал суммируется со случайной последовательностью, имитирующей собственные шумы стробоскопического смесителя.

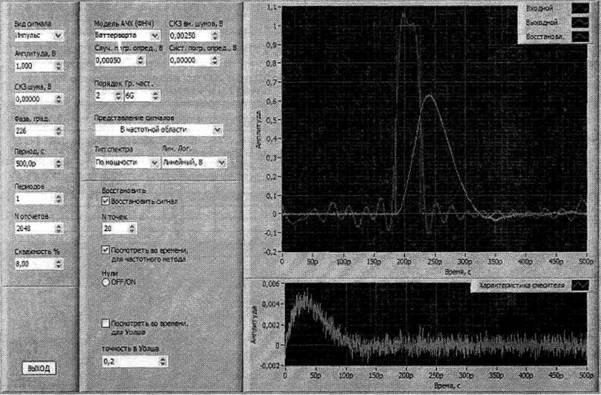
Рис. 3 - Внешний вид окна управляющей программы. Восстановление формы импульса длительностью 40 пс (ширина спектра главного лепестка 25 ГГц), воздействующего на вход осциллографа с полосой пропускания 6 ГГц

Задача восстановления сигналов во временной области в большинстве случаев является некорректно поставленной. Реально присутствующая погрешность измерения и внутренние шумы смесителя вызывают сильный разброс решения (рис. 4). Учитывая возможность накопления и усреднения значений полученного решения, этот метод позволяет уверенно регистрировать сигналы при 2 - 3-х кратном расширении полосы пропускания.

Метод требует высокой производительности вычислительных устройств.

Ниже на рис. 4 представлены аналогичные сигналы при восстановлении в частотной области. Отличительной особенностью этого метода является возможность установления «желаемого порогового» значения верхней граничной частоты восстановления. Это позволяет исключить наиболее зашумленные высокочастотные составляющие сигнала. Форма восстановленного сигнала, таким образом, не будет в полной мере повторять форму входного.

На рис. 5 показан разный порог верхней граничной частоты восстановления, и соответствующая форма этих сигналов во временной области.

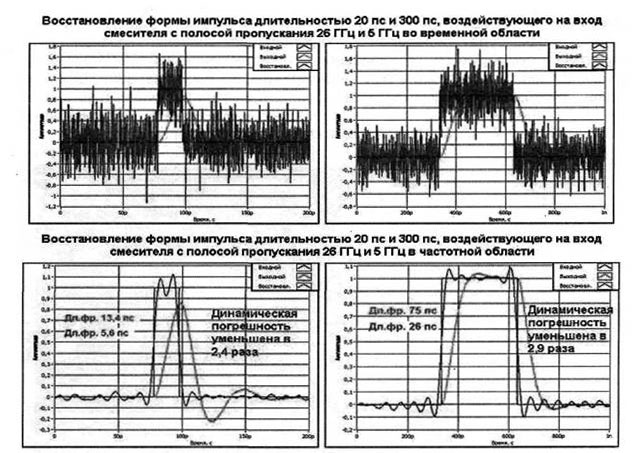
Рис.4

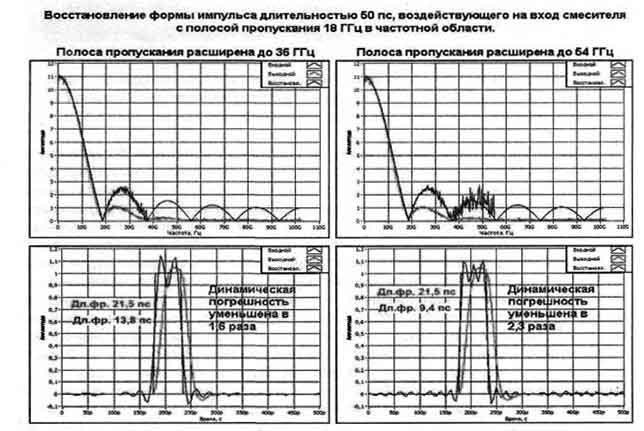
Рис. 5

Внедрение решения. Используемое оборудование и программное обеспечение National Instruments

В дальнейшем была проведена апробация методов восстановления формы сигналов на цифровом осциллографе Agilent 81204B DSO. Это цифровой осциллограф реального времени, частотный коэффициент передачи которого очень резко уменьшается на частотах выше верхней граничной частоты полосы пропускания. Однако данный факт влияет лишь на количественную оценку величины расширения полосы пропускания и не мешает показать саму возможность ее расширения.

С помощью формирователя эталонного перепада напряжения с длительностью фронта 20 пс снималась переходная характеристика осциллографа Agilent 81204B DSO, предварительно включенного в режим пониженной полосы пропускания 1 ГГц (рис. 6). Затем путем дифференцирования находилась его импульсная характеристика, и вычислялся комплексный коэффициент передачи.

При измерении параметров импульса длительностью 750 пс, имеющего длительность фронта не более 150 пс, (ширина спектра главного лепестка 1,333 ГГц), его форму удалось восстановить в частотном диапазоне до 1,3 ГГц (рис. 8) и с небольшими искажениями в частотном диапазоне до 2,75 ГГц (рис. 9).

Рис. 6

Программное обеспечение автоматизированной системы (рис. 7) разработано в среде программирования LabVIEW 8.0. Управление осциллографом выполнялось с помощью интерфейсной платы GPIB-USB-B производства фирмы National Instruments.

Применение среды LabVIEW с использованием технологии виртуальных приборов позволило значительно упростить и сократить время разработки модели прохождения сигналов через стробоскопический осциллограф, а также системы автоматизации осциллографа Agilent 81204B DSO.

В первом случае удобство для задач моделирования заключалось в возможности использования встроенных функций высокого уровня. Таких как, генерация последовательностей данных, цифровая фильтрация сигнала, операции свертки и обратной свертки, БПФ и обратное БПФ, интегрирование и дифференцирование, функции работы с массивами и кластерами. Особое значение для задач метрологии имело наличие встроенных функций генерации псевдослучайных последовательностей с различными вероятностными характеристиками для имитации различного вида шумов.

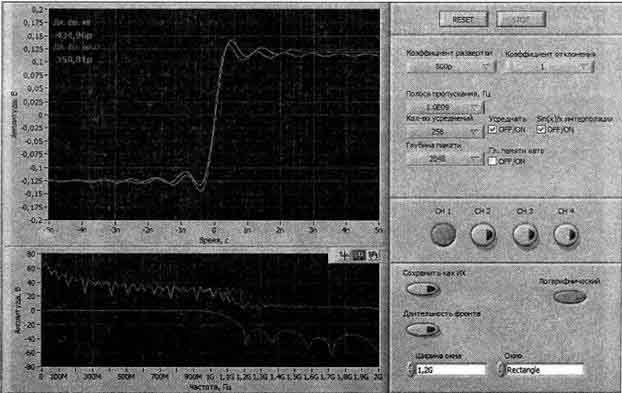
Рис. 7 Внешний вид окна программы, управляющей цифровым осциллографом . Agilent 81204В DSO

При разработке системы автоматизации осциллографа Agilent 81204B DSO, применение среды LabVIEW и встроенных функций для управления измерительными приборами с помощью контроллера GPIB значительно облегчило задачу программирования. Принцип модульности позволит в дальнейшем без особых проблем перенести разработанные методы восстановления на другие осциллографы.

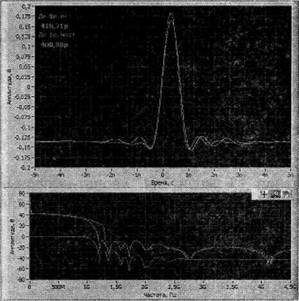
Рис. 8

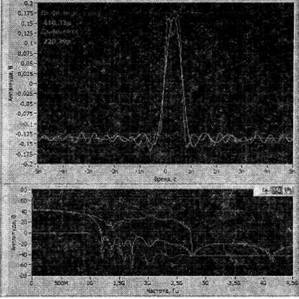
Рис. 9

Таким образом, по результатам математического моделирования установлено, что разработанные и реализованные на алгоритмическом и программном уровне методы восстановления формы входных сигналов позволяют измерять амплитудно-временные параметры сигналов в полосе частот в 2 - 3 раза превышающей полосу пропускания сверхширокополосного стробоскопического осциллографа.

Реализуемость методов восстановления формы сигналов и возможность расширения полосы пропускания осциллографов за счет априорной информации об их характеристиках подтверждается экспериментальными данными.

Разработанные методы восстановления целесообразно использовать для эталонных средств измерений амплитудно-временных параметров сверхкоротких импульсов.

Список литературы:

1.С.И. Баскаков, «Радиотехнические цепи и сигналы» - 2-е изд., перераб. и доп. - М.: Высшая школа, 1988;

2.А.Ф. Верлань, B.C. Сизиков, Справочное пособие «Интегральные уравнения: методы, алгоритмы, программы» - Киев: Наукова думка, 1986.

....................................................................................................