1. Постановка задачи

Разработка виртуальных инструментов в среде LabVIEW для исследования характеристик адаптивных эквалайзеров каналов связи.

2. Описание решения

Сегодня информационные технологии - это неотъемлемый элемент жизнедеятельности современного человека. Например, наличие высокоскоростного доступа к глобальной сети Интернет на работе, в дороге и дома уже давно стало нормой. Этому способствует большое разнообразие современных средств связи, которые постоянно развиваются в направлении повышения скорости передачи данных. Для передачи цифровых данных в связном оборудовании используются модемы. В составе большинства модемов имеется адаптивный выравниватель (эквалайзер) канала связи [1]. Он уменьшает уровень помех, обусловленных особенностями канала, в результате чего скорость передачи данных повышается. Параметры эквалайзеров во многом зависят от свойств канала связи. Поэтому при проектировании модемов часто приходится проводить исследования, связанные с определением этих параметров.

Представленные в настоящей работе виртуальные инструменты позволяют проводить такие исследования. Инструменты реализованы на языке графического программирования LabVIEW [2]. Графические возможности этого языка позволяют создавать наглядные переключатели, средства ввода-вывода цифровых данных, а также средства вывода графиков. Вычислительные процедуры: алгоритмы адаптивной фильтрации, расчет импульсных откликов канала связи, формирование сигналов, оценка параметров сигналов и показателей качества работы адаптивных фильтров реализованы в виде программ на языке математического моделирования MATLAB [3].

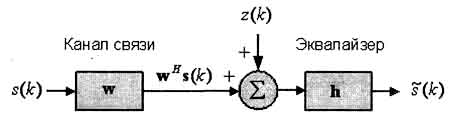
Рис. 1. Принцип выравнивания канала связи

Совместное использование двух языков программирования позволяет выполнять моделирование в несколько раз быстрее по сравнению с аналогичным моделированием на языке MATLAB. Ускорение моделирования достигается за счет того, что в оперативное запоминающее устройство компьютера загружаются не все приложения языка MATLAB и осуществляется оптимизация переменных в соответствии с их типом.

При передаче цифровых данных по каналам связи с ограниченной полосой пропускания возникает явление, называемое межсимвольной интерференцией. Межсимвольная интерференция, наряду с шумом z(k) (рис. 1), сказывается на правильности решения о соответствии принятого информационного символа s^~(k) символу s(k), переданному по каналу связи с импульсным откликом w.

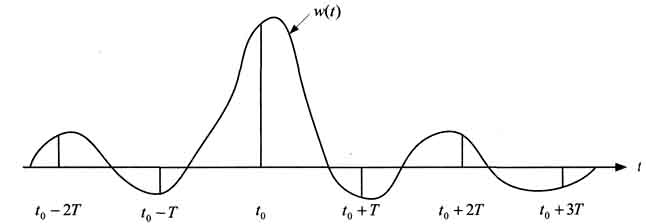
Рис. 2. Импульсный отклик канала связи

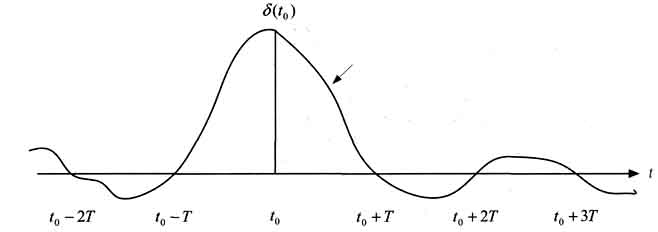
Рис. 3. Импульсный отклик: канал связи + эквалайзер

Если бы канал связи представлял собой просто линию задержки на время t₀, то принимаемый сигнал (информационные символы) можно было бы легко оценивать (различать). Однако большинство каналов связи с математической точки зрения представляют собой фильтр с импульсным откликом w (рис. 2). Поэтому в каждый отсчет времени к, совпадающий с моментом смены информационных символовТ, на выходе канала образуется взвешенная сумма передаваемых подряд символов:

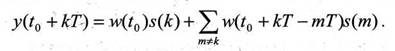
В данной сумме только один символ несет интересуемую информацию, а остальные являются шумом - межсимвольной интерференцией. Шум не позволяет правильно различать символы на приемной стороне. Чтобы повысить вероятность правильного решения относительно принимаемых символов используются устройства, именуемые эквалайзерами [1]. Эквалайзер функционирует таким образом, что его амплитудно-частотная характеристика (АЧХ) становится близкой к обратной АЧХ канала связи. Другими словами, совместная АЧХ канала связи и эквалайзера становится близкой к равномерной. Это означает, что свертка импульсных откликов канала связи w и эквалайзера h в моменты времени кТ близка к дельта-функции (рис. 3), в результате чего межсимвольная интерференция уменьшается. В этом случае выходной сигнал эквалайзера определяется как y(t₀ + kT) = σ(t_o)s(k) + 0, т.е. может быть правильно оценен.

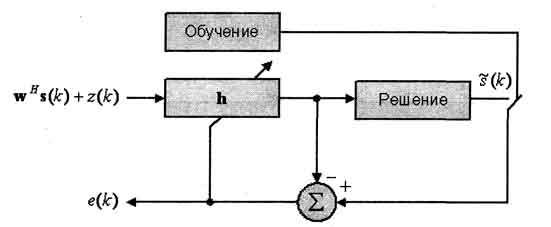
Рис. 4. Адаптивный эквалайзер без обратной связи

Существуют два основных типа адаптивных эквалайзеров. Это эквалайзер без обратной связи (Feed-Forward, FF) (рис. 4) и с обратной связью (Feed-Backward, FB) (рис. 5). В начале сеанса связи передается известная последовательность информационных символов, которая используется для обучения. После обучения эквалайзер функционирует на основе символов, которые оцениваются по значениям его выходного сигнала.

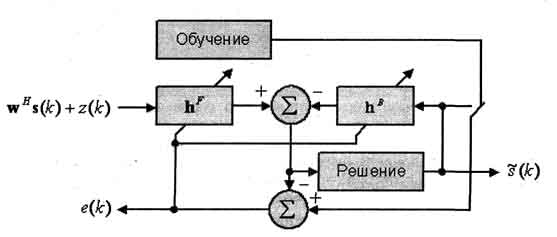
Рис. 5. Адаптивный эквалайзер с обратной связью

Эквалайзеры строятся на основе адаптивных фильтров. В таких фильтрах на каждой итерации к изменяются весовые коэффициенты h_N(k) = f{x_N(k),h_N(k-l),d(k)}. Здесь d(k) -требуемый сигнал, h_N(k) - вектор весовых коэффициентов, x_N(k) - вектор входных сигналов и N - число весовых коэффициентов адаптивного фильтра. Одноканальный адаптивный фильтр используется для построения эквалайзеров без обратной связи, а для построения эквалайзера с обратной связью используется двухканальный адаптивный фильтр.

В качестве алгоритмов адаптивной фильтрации обычно применяется простейший с вычислительной точки зрения нормализованный алгоритм по критерию наименьшего среднеквадратичного отклонения (Normalized Least Mean Squares, NLMS) или используются более сложные, но и более эффективные рекурсивные адаптивные алгоритмы по критерию наименьших квадратов (Recursive Least Squares, RLS) [4].

Для эквалайзера требуется определять ряд таких параметров, как число весовых коэффициентов адаптивного фильтра (в случае FF-эквалайзера), соотношение между числом весовых коэффициентов в прямой h^F и обратной ветвях эквалайзера h^B (в случае FB-эквалайзера), алгоритм адаптивной фильтрации. Эффективность работы эквалайзера зависит от вида передаточной функции канала связи (ее обратимости) и уровня шума z(k).

Передаточная функция и импульсный отклик связаны между собой преобразованием Фурье. Они вычисляются на основе параметров канала связи.

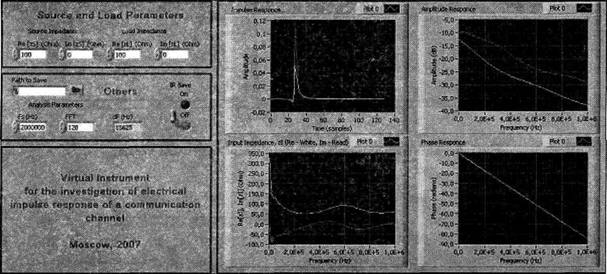
Рис. 6. Калькулятор электрического импульсного отклика

Импульсный отклик проводного канала связи описывается линейными четырехполюсниками из сосредоточенных (резисторы, конденсаторы, индуктивности) и распределенных (проводные линии связи) элементов [5, 6]. В основе работы калькулятора электрического импульсного отклика (рис. 6) находится теория линейных четырехполюсников, характеризуемых ABCD-параметрами.

Напряжения и токи на выводах четырехполюсника, (рис. 7) зависят от напряжения источника U_s, импеданса источника Z_s и импеданса нагрузки Z_L. Они всегда удовлетворяют соотношению

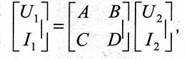
где ABCD-параметры находятся путем анализа режимов короткого замыкания и холостого хода четырехполюсника как А = U₁/U₂ |_I2=0. В = U₁/I₂ |_V2=0, C= I₁/U₂ |_I2=0 и D= I₁/I₂ |_V2=0;

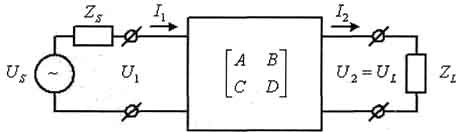
Рис. 7. Линейный четырехполюсник

Четырехполюсники, характеризуемые ABCD-параметрами, широко используются при моделировании каналов связи, так как такие каналы всегда можно представить в виде последовательного соединения различных четырехполюсников, а матрица ABCD-параметров последовательного соединения (рис. 8) равна произведению матриц отдельных четырехполюсников:

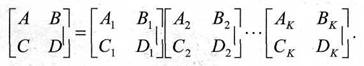
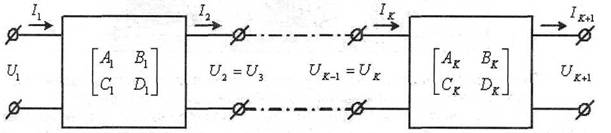
Рис. 8. Последовательное соединение линейных четырехполюсников

При вычислении импульсного отклика в калькуляторе (рис. 6) с помощью графических средств задаются частота дискретизации, импеданс источника сигнала и нагрузки четырехполюсника. Длительность моделируемых электрических импульсных откликов определяется частотой дискретизации сигналов и числом точек используемой процедуры преобразования Фурье. Топология и параметры отдельных четырехполюсников задаются в моделирующей программе. В калькуляторе визуализируются входной импеданс (действительная и мнимая части), импульсный отклик, АЧХ и фазочастотная характеристика (ФЧХ) функции потерь, а также импульсный отклик, АЧХ и ФЧХ передаточной функции четырехполюсника. Импульсные отклики могут быть сохранены в mat-файле, а также использованы в инструменте (рис. 9).

Рис. 9. Виртуальный инструмент для исследования адаптивного эквалайзера: результаты моделирования эквалайзера с обратной связью.

Виртуальный инструмент (рис. 9) для исследования характеристик эквалайзера разработан в среде LabVIEW с использованием основных вычислительных процедур, реализующих модели передаваемых сигналов, эквалайзера, расчета вероятности принятых ошибочно информационных символов и ошибочных бит (Symbol Error Rate, SER, и Bit Error Rate, BER) на языке MATLAB. В инструменте реализована квадратурная амплитудная модуляция. Можно выбирать алгоритм адаптивной фильтрации (NLMS или RLS), тип эквалайзера (FF или FB), задавать параметры адаптивного фильтра, алфавит (созвездие) передаваемых символов, отношение сигнал-шум на входе эквалайзера, задержку обучающей последовательности относительно передаваемой последовательности, число обучающих символов и число символов, передаваемых после обучения. Параметры SER и BER оцениваются на основе символов, передаваемых после обучения эквалайзера.

В качестве результатов моделирования в виртуальном инструменте выводятся численные значения SER и BER. В графическом виде выводятся созвездия: передаваемых информационных символов, символов на выходе канала связи без шума и с шумом, а также символов на выходе эквалайзера. Созвездия позволяют определять расстояние между передаваемыми и принимаемыми символами. На панели инструмента также отображаются импульсный отклик и АЧХ канала связи, эквалайзера, свертка импульсных откликов канала связи и адаптивного эквалайзера, общая АЧХ канала связи и эквалайзера.

Дополнительные сведения о рассмотренных инструментах приведены в работах [7, 8].

3. Используемое оборудование и ПО

Проекты инструментов реализованы на языках LabVIEW 7.0 и MATLAB 7.0. Для выполнения проектов требуется программное обеспечение указанных или более высоких версий. Специальные требования к ресурсам используемого персонального компьютера не предъявляются. Эти требования определяются указанным программным обеспечением.

4. Перспективы внедрения и развития решения - отрасли, названия предприятий, и т.п.

Представленные в работе инструменты использованы в Государственном унитарном предприятии г. Москвы «Научно-производственный центр «Электронные вычислительно-информационные системы», в Московском физико-технический институте (государственном университете) и Самарском государственном университете путей сообщения.

Инструменты могут применяться при исследовании и проектировании выравнивателей каналов связи, а также при проведении лабораторных работ.

Инструменты являются открытыми, что позволяет модифицировать и расширять их функциональные возможности: применять различные типы модуляции, различные алгоритмы адаптивной фильтрации, и т.п.

Список литературы

1. S. Qureshi. Adaptive equalization // IEEE Signal Processing Magazine. - 1982.-№3.-P. 9-16.

2. Л.Г. Белиовская, А.Е. Белиовский. LabVIEW — школьный курс. - M.: National Instruments, 2006. - 200 с. v > ^ ^ ;

3. E.P. Алексеев. MATLAB 7. - M: HT Пресс, 2006. - 464 с.

4. Б. Уидроу, С. Стирнз. Адаптивная обработка сигналов. Пер. с англ. под ред. Шахгильдяна В.В. - М.: Радио и связь, 1989. -440 с.

5. W.Y.Chen. Simulation techniques and standards development for digital subscriber line systems. - IN: Indianapolis, Macmillan Technical Publishing, 1998.-644 p.

6. Cable reference models for simulating metallic access networks // Document 970p02r3. ETSI STC TM6 Meeting. Luea, Sweden, 22-26 June 1998. - 40 p.

7. Л.Г. Белиовская, М.В. Джиган, О.В. Джиган. Калькуляторы импульсных откликов // Материалы 15-й Международной конференции «Информационные средства и технологии». - Москва, 2007. - Том 1. - С. 72-75.

8. Л. Белиовская, М. Джиган, О. Джиган. Совместное использование пакетов LabVIEW и MATLAB в задачах эхокомпенсации и выравнивания каналов связи // Современная электроника. - 2007. - №3. - С. 56-60.

..............................................................................................................................