1. Введение

В настоящее время двигатели внутреннего сгорания используются во всех областях народного хозяйства: промышленность и сельское хозяйство, гражданское и дорожное строительство, транспорт, энергетика, нефтяная промышленность и т.д. Двигатели используемых в этих областях мобильных и стационарных агрегатов работают при резко изменяющихся нагрузках [1]. Это происходит при трогании с места автомобилей и тракторов, переключении передач, преодолении препятствий, выполнении дорожно-строительных и сельскохозяйственных работ [1]. По литературным данным переменные режимы для автомобилей составляют в городе 97%, на грунтовых дорогах 92%, на загородных магистралях 34% процентов всего времени работы [1 имеющиеся в ней ссылки]. Переменные режимы тракторных двигателей возникают при транспортных работах, которые составляют 40-45% от общего времени работы, так и при выполнении основных сельскохозяйственных операций. Если при транспортных работах двигатели загружены резкопеременными нагрузками, обусловленными в основном изменением профиля дорог, то для сельскохозяйственных операций характерен режим при котором нагрузка колеблется относительно какого-то среднего значения.

Исследования показывают, что учет динамических характеристик двигателя позволяет повысить эксплуатационную мощность, экономичность, надежность, долговечность и понизить токсичность и износ двигателя внутреннего сгорания [2]. Потенциальные возможности использования результатов исследования ДВС при неустановившихся режимах составляет повышение экономичности 15-20%, производительность машинно-тракторных агрегатов на 15-20%. Из всего вышесказанного очевидна актуальность разработки стендов для исследования двигателей внутреннего сгорания при неустановившейся нагрузке. Вариант такого стенда рассматривается в данной работе.

2. Схема стенда для исследований рабочих процессов двигателя внутреннего сгорания в динамических режимах

Согласно техническому заданию разработанный стенд должен обеспечивать возможность определения динамических характеристик рабочих процессов двигателя в виде дифференциальных уравнений, описывающих реакции изменения частоты вращения коленчатого вала двигателя внутреннего сгорания, расхода воздуха и расхода топлива при изменении момента сопротивления на коленчатом валу двигателя внутреннего сгорания и позволять автоматическое проведение измерений и обработки информации.

Схема стенда для исследований рабочих процессов двигателя внутреннего сгорания в динамических режимах приведена на рис. 1. Стенд работает следующим образом.

После запуска двигателя внутреннего сгорания 4 электротормоз 2 создает постоянный тормозящий момент, воздействующий на коленчатый вал двигателя внутреннего сгорания 4. После достижения двигателем внутреннего сгорания 4 установившегося режима имитатор типовых нагрузок 1 по сигналу автоматизированного блока управления 14 вырабатывает сигнал, приводящий к изменению момента сопротивления электротормоза 2. Изменение тормозящего момента приводит к появлению переходных процессов: изменяется крутящий момент на валу двигателя 4, изменяется частота вращения коленчатого вала двигателя 4, изменяется расход топлива и воздуха.

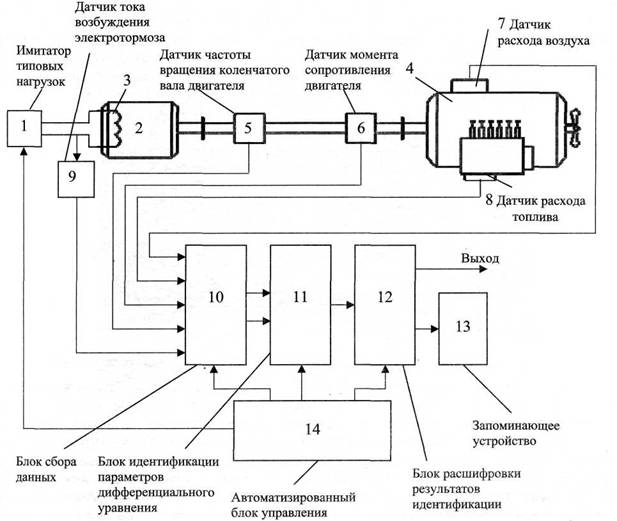
Рис. 1. Схема стенда для исследований рабочих процессов двигателя внутреннего сгорания в динамических режимах

Эти переходные процессы посредством датчиков преобразуются в электрические сигналы и поступают в блок сбора данных 10, который по команде автоматизированного блока управления 14 выдает на вход «сигнала отклика» блока идентификации параметров дифференциального уравнения один из четырех сигналов датчиков: датчика 5 частоты вращения коленчатого вала двигателя, датчика 6 момента сопротивления двигателя, датчика 7 расхода воздуха, датчика 8 расхода топлива, а на вход «сигнала» воздействия - сигнал с датчика 9 тока возбуждения электротормоза, при этом соответствующие сигналы преобразуются в цифровую форму. Сигналы, поступившие в блок идентификации параметров дифференциального уравнения 11, используются для определения параметров динамических моделей рабочих процессов двигателя внутреннего сгорания (коэффициентов дифференциального уравнения), при этом используются дифференциальных уравнений следующего вида: для регуляторной ветви регуляторной характеристики

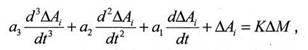
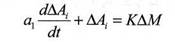
где a₁, a₂, a₃ - искомые коэффициенты дифференциального уравнения; ∆A_i - изменение наблюдаемого показателя двигателя внутреннего сгорания крутящего момента на валу двигателя, частоты вращения коленчатого вала двигателя, расхода топлива и воздуха при изменении нагрузки; AM - изменение момента сопротивления электротормоза; К - коэффициент пропорциональности.

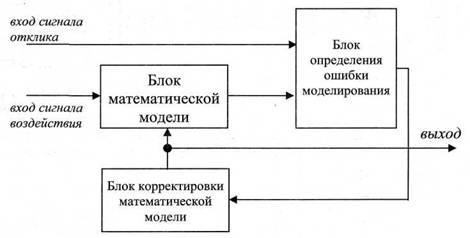
Рис. 2. Схема блока идентификации параметров дифференциального уравнения

Схема блока идентификации параметров дифференциального уравнения 11 приведена на рис. 2, данный блок работает следующим образом, сигнал с входа сигнала воздействия: изменение момента сопротивление электротормоза 2, поступает на блок математической модели, выходной сигнал блока математической модели поступает на вход блока определения ошибки моделирования, где он сравнивается с сигналом, поступившим на вход сигнала отклика, который соответствует реакции двигателя на воздействие - изменение либо момента сопротивления двигателя, либо частоты вращения коленчатого вала, либо расхода топлива, либо расхода воздуха, на основании этого блок определения ошибки моделирования вырабатывает сигнал, соответствующий рассогласованию математической модели и исследуемого объекта, данный сигнал поступает на вход блока корректировки математической модели, изменяющий параметры блока математической модели с целью уменьшить ошибку моделирования, коэффициенты, соответствующие минимуму ошибки моделирования, принимаются в качестве искомых коэффициентов. Полученные коэффициенты дифференциального уравнения поступают в блок расшифровки результатов идентификации 12, который определяет порядок используемого для идентификации дифференциального уравнения и представляет коэффициенты дифференциальных уравнений в форме удобной для дальнейшего использования. После этого динамические характеристики либо выдаются на выход потребителю, либо запоминаются в запоминающем устройстве 13. Работа стенда автоматизирована и управляется автоматизированным устройством управления 14.

Наличие в стенде для исследований рабочих процессов двигателей в динамических режимах блока идентификации параметров дифференциального уравнения, выполненного с двумя входами, позволяет снизить влияние неидеальности воздействия вызванного инерционностью электротормоза на определяемые динамические характеристики рабочих процессов двигателя внутреннего сгорания. Наличие блока расшифровки результатов идентификации позволяет сформировать дифференциальное уравнение для каждого из исследуемых рабочих процессов: частота вращения коленчатого вала, расход воздуха, расход топлива и предоставить его потребителю. Программное обеспечение данного стенда было написано на LabVIEW лицевая панель главной программы изображена на рис. 3.

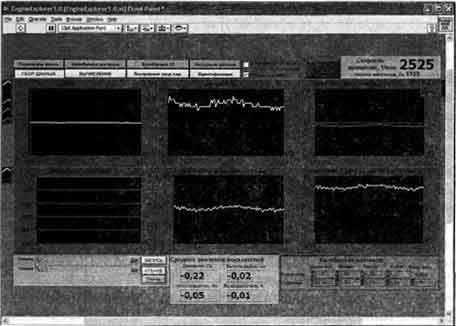
Рис. 3. Лицевая панель программы

3. Идентификация дифференциального уравнения второго порядка

Рассмотрим подробнее задачу идентификации параметров дифференциального уравнения описывающего динамические характеристики ДВС. Данная задача формулируется следующим образом.

Требуется, используя информацию о воздействие x(t) на исследуемый объект и об его отклике y(t), определить параметры 7V, Т₂, к математической модели М описываемой дифференциальным уравнением третьего порядка (для регуляторной ветви регуляторной характеристики, мы будем рассматривать только его как наиболее общий):

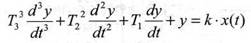
Пронормируем дифференциальное уравнение

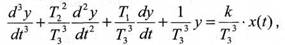
или

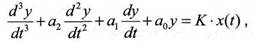
где

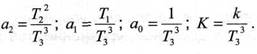
Рассмотрим способ идентификации по замкнутой схеме (рис.2). В этом случае задача нахождения коэффициентов дифференциального уравнения (5) сводится к задаче оптимального управления коэффициентами a₂, a₁, a₀.

Пусть в результате измерения получена реализация выходного сигнала системы y(t)=f(t, a₂, a₁, a₀) в ответ на входное воздействие x(t) (здесь a₂, a₁, a₀ -неизвестные параметры системы). Зададимся параметрами модели a₂^м, a₁^м, a₀^м. Тогда входному сигналу x(t) будет соответствовать выходной сигнал модели y_M(t)=f_M(t, a₂^м, a₁^м, a₀^м). Следовательно, ошибку идентификации е можно определить согласно следующему выражению.

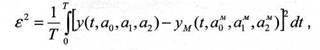
Очевидно, что ошибка ε будет минимальна при совпадении искомых коэффициентов ε с соответствующими параметрами исследуемого процесса a₂^м →a₂ , a₁^м →a₁, a₀^м →a₀ => ε ²→0. Следовательно, задачу определения коэффициентов дифференциального уравнения, можно свести к задаче оптимального управления коэффициентами a₂^м, a₁^м, a₀^м. Оптимальное управление состоит в следующем: путем регулирования коэффициентами a₂^м, a₁^м, a₀^м найти такие коэффициенты дифференциального уравнения при которых ошибка ε ²=f(a₂^м, a₁^м, a₀^м,a₂, a₁, a₀) будет минимальной.

Алгоритм идентификации (определения параметров) приведен на рис.4.

Входное воздействие поступает одновременно на вход исследуемого объекта и его модели. На основании их выходных сигналов y(t), y_M(t) определяется ошибка моделирования ε. Ошибка ε используется для коррекции (регулировки) параметров модели a₁^м, a₀^м, с целью ее уменьшения.

В качестве искомых параметров модели примем параметры a₁^м, a₀^м для которых ошибка ε минимальна.

Таким образом, процесс определения параметров модели сводится к двум операциям:

• Моделирование;

• Определение ошибки моделирования и коррекция (регулировка) параметров модели.

Остановимся на этих этапах подробнее.

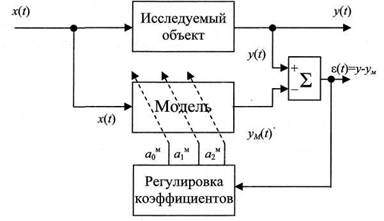
Рис.4. Алгоритм определения параметров модели

• Моделирование (Численное решение дифференциального уравнения) Как отмечалось выше нам задано дифференциальное уравнение третьего порядка:

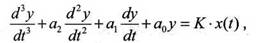
где x(t) - функция, определяющая воздействие на вход системы; y(t) - функция

(выходной отклик системы);

a₂, a₁, a₀, К- постоянные коэффициенты.

При моделировании нам задаются следующие величины

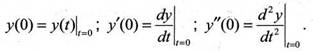
3. начальные условия

1. воздействие x(t);

2. параметры a₂, a₁, a₀ , К; ;

Требуется найти выходной сигнал y(t) системы при заданных выше условиях Разрешим уравнение (7) относительно старшей производной:

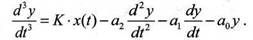
Такое дифференциальное уравнение (8) может быть смоделировано согласие следующей схеме рис. 5.

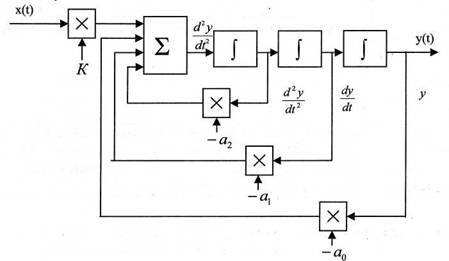
Рис. 5. Структурная схема численного решения дифференциального уравнения.

Входное воздействие x(t) умножается на весовой коэффициент К. После этого сигнал поступает на вход сумматора. На два других входа сумматора, подаются сигналы с выхода первого интегратора d²y/dt², с выхода второго интегратора dy/dt выходной сигнал y(t) с соответствующими весовыми коэффициентами -a₂, -a₁, -a₀. На выходе сумматора согласно выражению (8) получим третью производную выходного сигнала системы. Дважды интегрируя этот сигнал, получаем выходной сигнал системы - решение дифференциального уравнения.

Подпрограмма LabVIEW, выполняющая численное решение дифференциального уравнения согласно приведенному выше алгоритму изображена на рис.6.

• Минимизация функционала (коррекция коэффициентов дифференциального уравнения)

Управление коэффициентами дифференциального уравнения, как было отмечено выше, осуществляется с целью минимизировать ошибку моделирования ε.

Ошибку моделирования ε можно представить, как функцию нескольких переменных

ε ²=f(a₂^м, a₁^м, a₀^м,a₂, a₁, a₀)

Переменные a₁, a₀ однозначно определяются параметрами исследуемого объекта, и в процессе идентификации считаются постоянными. Поэтому в нашем случае, ошибку моделирования можно представить как функцию меньшего числа переменных:

ε ²=f(a₂^м, a₁^м, a₀^м) .

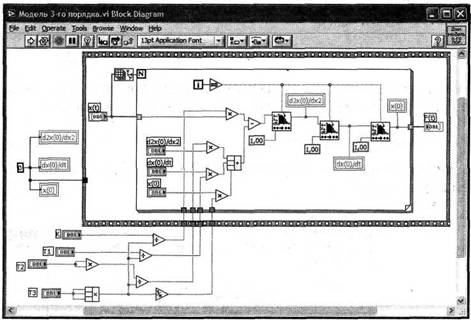
Рис. 6. Подпрограмма численного решения дифференциального уравнения в LabVIEW.

Следовательно, можно использовать широко известные методы поиска минимума функции нескольких переменных. В качестве такого метода выберем «метод покоординатного спуска» (метод Гаусса - Зейделя).

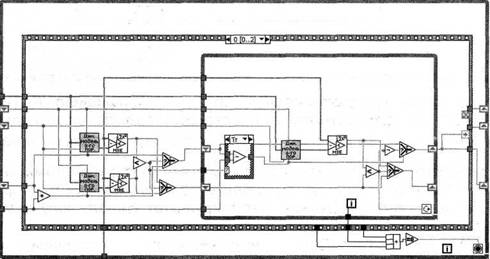
Рис. 7. Цикл, осуществляющий минимизацию функционала согласно алгоритму Гаусса - Зейделя в LabVIEW

Суть этого метода заключается в следующем:

1. Выбираем некоторые начальные коэффициенты a₂⁰, a₁⁰, a₀⁰

2. После этого мы фиксируем два коэффициента, a₁, a₀ и производим поиск минимума ошибки ε при изменении коэффициента a₂. Коэффициент a₂ соответствующий минимуму принимается, за новое приближенное значение коэффициента a₂.

3. Далее повторяется процедура аналогичная описанной в п.2. Но при этом фиксируется параметры a₂ и a₀, и ищется минимум функции при изменении a₁.

4. Далее повторяется процедура аналогичная описанной в п.2. Но при этом фиксируется параметры a₂ и a₁, и ищется минимум функции при изменении a₀.

5. Повторяется п. 2

6. Процесс останавливается если при выполнении п.2, п.З и п.4 коэффициенты a₂, a₁, a₀ изменились не более чем на определенную величину ∆. И эти коэффициенты принимаются в качестве искомых параметров модели

Цикл, осуществляющий минимизацию функционала согласно алгоритму Гаусса - Зейделя в LabVIEW, изображен на рис. 7.

Все описанные алгоритмы были реализованы в программной среде LabVIEW, что позволило производить автоматизированное определение искомых параметров.

4. Выводы

Описанный в данной работе стенд может быть использован при исследовании рабочих процессов двигателей внутреннего сгорания в динамических режимах (в условиях эксплуатации). На предлагаемом стенде обеспечивается возможность определения динамических характеристик рабочих процессов двигателя в виде дифференциальных уравнений, описывающих реакции изменения частоты вращения коленчатого вала двигателя, момента сопротивления двигателя, расхода воздуха и расхода топлива при изменении момента сопротивления на коленчатом валу двигателя, при этом процесс измерения и обработки информации автоматизирован. Программное обеспечение реализовано в программной среде LabVIEW. Выбор данной программной среды для реализации приведенного выше алгоритма обусловлен следующими важными факторами:

• На языке графического программирования LabVIEW, именуемого "G", программы создаются в виде блок-схемы, которые являются естественной формой проектирования.

• Обширная библиотека анализа данных содержит функции генерации сигналов, их обработки, фильтрации, статистической оценки параметров, что существенно облегчает решение поставленных задач.

• LabVIEW позволяет создавать удобный пользовательский интерфейс.

• Наглядность обработки сигналов.

Литература

1. Юлдашев А.К., Хайрутдинов И.Н. Стенды для исследования двигателей внутреннего сгорания при неустановившихся нагрузках. - Казань: Изд-во «Фэн», 2002.

2. Использование динамических характеристик рабочих процессов тепловых двигателей для проектирования, эксплуатации, диагностики и ремонта: Материлы международного научно-технического семинара, Казань, 22-25 сентября 2003 года.

3. Евдокимов Ю.К., Линдваль В.Р., Щербаков ПИ. LabVIEW для радиоинженеров: от виртуальной модели до реального прибора. Практическое руководство для работы в программной среде LabVIEW. - М: ДМК Пресс, 2007. - 400 с.

4. Патент на полезную модель (РФ) № 66526 Стенд для исследования рабочих процессов двигателя внутреннего сгорания в динамических режимах/ Юлдашев А.К., Евдокимов Ю.К., Синицкий С.А., Денисов ЕС. и д.р. 10.9.2007 Бюл. №25

..............................................................................................................................